Simplifying Fractions Gcse Maths Steps Examples

Simplifying Fractions Gcse Maths Steps Examples 2. 2 divide both the numerator and the denominator by the hcf. 10 \div 2=5 10 ÷2 = 5 14 \div 2=7 14 ÷2 = 7. the new numerator is 5 5 and the new denominator is 7. 7. 5 5 and 7 7 have no common factors other than 1. 1. so the fraction will be in its simplest form. 3 write the fraction in its simplest terms. We can also use equivalent fractions to find a common denominator by multiplying both the numerator and the denominator by the same number. this is very useful for adding fractions, subtracting fractions and ordering fractions. step by step guide: equivalent fractions. see also: simplifying fractions.

Simplifying Algebraic Fractions Gcse Maths Steps Examples Example 3: linear ÷ linear. simplify the algebraic fraction. \frac {6x 12} {10x 20} 10x 206x 12. complete any calculations required in the question ( −\times\div) ( − × ÷). show step. here there is no calculation to complete as we have a single fraction. factorise the numerator and the denominator. The common factors of 8 and 28 are 1, 2, and 4. dividing the numerator and denominator by the common factors. on dividing the numerator and denominator by 2, we get. 8 ÷ 2 28 ÷ 2 = 4 14. again, by dividing the numerator and denominator by 2, we get. 4 ÷ 2 14 ÷ 2 = 2 7, which is in its simplest form. thus, 8 28 is simplified to 2 7. When simplifying a fraction you must divide the numerator and the denominator by the same number. 12 ÷ 6 30 ÷ 6 = 2 5 \dfrac{12\div 6}{30\div 6}=\dfrac{2}{5} 3 0 ÷ 6 1 2 ÷ 6 = 5 2 you can see that the same number is used for both the numerator and the denominator. They all represent the same amount of a whole. if you multiply the top (the numerator) and the bottom (the denominator) by the same number you get an equivalent fraction. example 1: write down 5 fractions equivalent to 2 3. we can multiply the numerator and the denominator by 2: 2 × 2 = 4. 3 × 2 = 6. 2 3 = 4 6.

Simplifying Fractions Examples How To Simplify Fractions When simplifying a fraction you must divide the numerator and the denominator by the same number. 12 ÷ 6 30 ÷ 6 = 2 5 \dfrac{12\div 6}{30\div 6}=\dfrac{2}{5} 3 0 ÷ 6 1 2 ÷ 6 = 5 2 you can see that the same number is used for both the numerator and the denominator. They all represent the same amount of a whole. if you multiply the top (the numerator) and the bottom (the denominator) by the same number you get an equivalent fraction. example 1: write down 5 fractions equivalent to 2 3. we can multiply the numerator and the denominator by 2: 2 × 2 = 4. 3 × 2 = 6. 2 3 = 4 6. A video explaining how to simplify algebraic fractions by factorising. exam question booklets:📝🔗exam question edexcel style: 1stclassmaths. Simplifying fractions is important. you could go into a cake shop and ask for 50 200 of a cake, but you'd probably get a funny look! 50 200 is, of course, the same as a quarter! let's see why: firstly we can remove a power of ten from the top and bottom of the fraction. in other words, cross off a zero.

Simplifying Algebraic Fractions Gcse Maths Steps Examples A video explaining how to simplify algebraic fractions by factorising. exam question booklets:📝🔗exam question edexcel style: 1stclassmaths. Simplifying fractions is important. you could go into a cake shop and ask for 50 200 of a cake, but you'd probably get a funny look! 50 200 is, of course, the same as a quarter! let's see why: firstly we can remove a power of ten from the top and bottom of the fraction. in other words, cross off a zero.

Simplifying Algebraic Fractions Gcse Maths Steps Examples

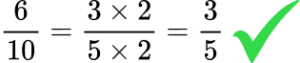
Simplifying Fractions Gcse Maths Steps Examples