Simple Linear Regression Maximum Likelihood Estimation

Ppt Simple Linear Regression Powerpoint Presentation Free Download We introduced the method of maximum likelihood for simple linear regression in the notes for two lectures ago. let’s review. we start with the statistical model, which is the gaussian noise simple linear regression model, de ned as follows: 1.the distribution of xis arbitrary (and perhaps xis even non random). 2.if x = x, then y = 0. The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is.
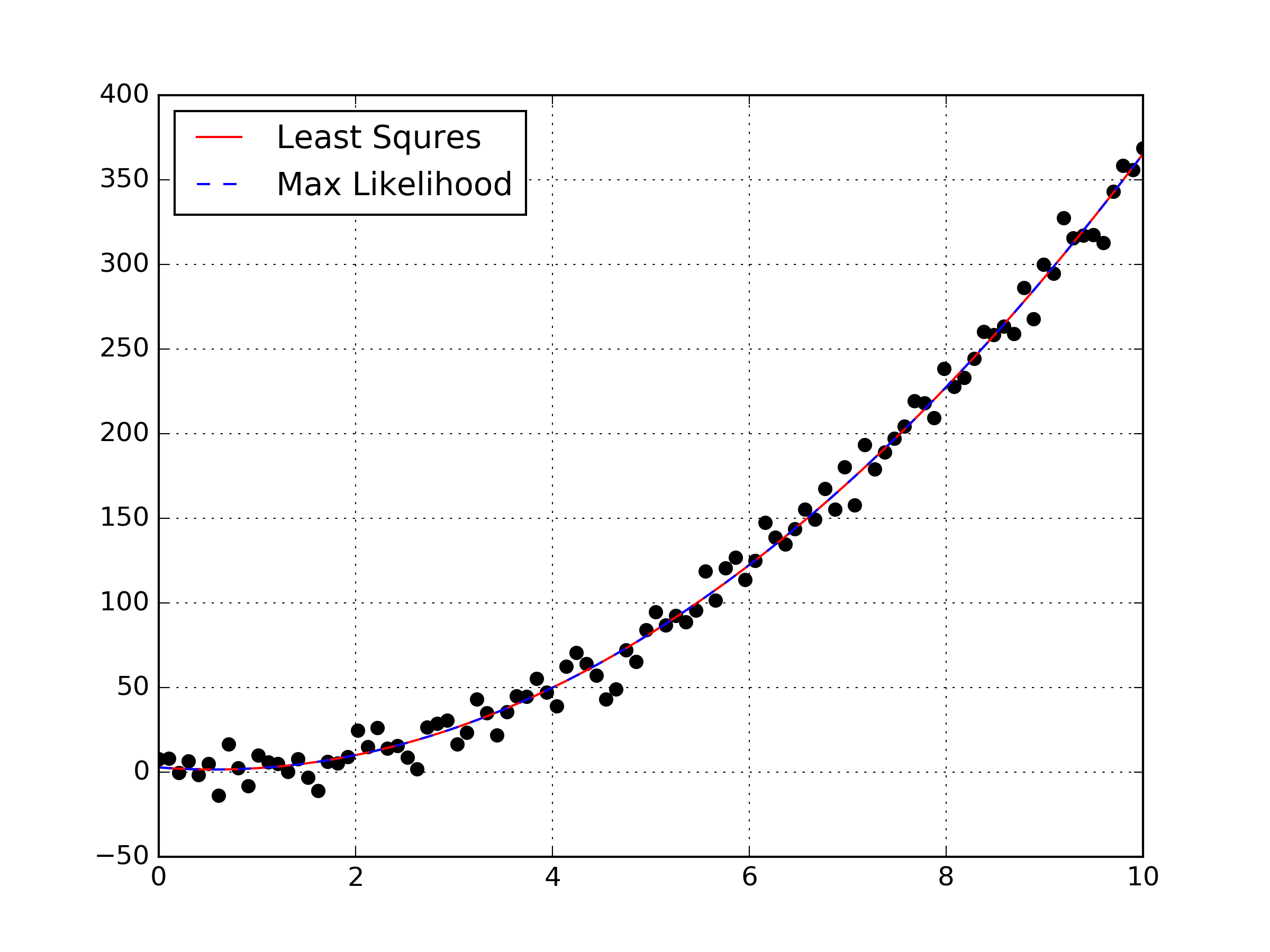
Charles Jekel Jekel Me Maximum Likelihood Estimation Linear Regression Index: the book of statistical proofs statistical models univariate normal data simple linear regression maximum likelihood estimation . theorem: given a simple linear regression model with independent observations \[\label{eq:slr} y i = \beta 0 \beta 1 x i \varepsilon i, \; \varepsilon i \sim \mathcal{n}(0, \sigma^2), \; i = 1,\ldots,n. It can be shown (we'll do so in the next example!), upon maximizing the likelihood function with respect to μ, that the maximum likelihood estimator of μ is: μ ^ = 1 n ∑ i = 1 n x i = x ¯. based on the given sample, a maximum likelihood estimate of μ is: μ ^ = 1 n ∑ i = 1 n x i = 1 10 (115 ⋯ 180) = 142.2. pounds. Properties of mle. maximum likelihood estimator : = arg max. best explains data we have seen. does not attempt to generalize to data not yet observed. often used when sample size is large relative to parameter space. potentially biased (though asymptotically less so, as → ∞) consistent: lim 9 − < = 1 where > 0. f. Linear regression is a classical model for predicting a numerical quantity. the parameters of a linear regression model can be estimated using a least squares procedure or by a maximum likelihood estimation procedure. maximum likelihood estimation is a probabilistic framework for automatically finding the probability distribution and parameters that best describe the observed data. supervised.

Simple Linear Regression Maximum Likelihood Estimation Youtube Properties of mle. maximum likelihood estimator : = arg max. best explains data we have seen. does not attempt to generalize to data not yet observed. often used when sample size is large relative to parameter space. potentially biased (though asymptotically less so, as → ∞) consistent: lim 9 − < = 1 where > 0. f. Linear regression is a classical model for predicting a numerical quantity. the parameters of a linear regression model can be estimated using a least squares procedure or by a maximum likelihood estimation procedure. maximum likelihood estimation is a probabilistic framework for automatically finding the probability distribution and parameters that best describe the observed data. supervised. Estimated regression line •using the estimated parameters, the fitted regression line is yˆ i= b0 b1xi where yˆ i is the estimated value at xi (fitted value). •fitted value yˆ iis also an estimate of the mean response e(yi) •yˆ i= pn j=1(˜kj xikj)yj= pn j=1 ˇkijyjis also a linear estimator •e(yˆ i) = e(b0 b1xi) = e(b0) e(b1)xi. Maximum likelihood estimation 1.the likelihood function can be maximized w.r.t. the parameter(s) , doing this one can arrive at estimators for parameters as well. l(fx ign =1;) = yn i=1 f(x i;) 2.to do this, nd solutions to (analytically or by following gradient) dl(fx ign i=1;) d = 0.

Solved 3 Fox 6 5 Maximum Likelihood Estimation Of The Simple Estimated regression line •using the estimated parameters, the fitted regression line is yˆ i= b0 b1xi where yˆ i is the estimated value at xi (fitted value). •fitted value yˆ iis also an estimate of the mean response e(yi) •yˆ i= pn j=1(˜kj xikj)yj= pn j=1 ˇkijyjis also a linear estimator •e(yˆ i) = e(b0 b1xi) = e(b0) e(b1)xi. Maximum likelihood estimation 1.the likelihood function can be maximized w.r.t. the parameter(s) , doing this one can arrive at estimators for parameters as well. l(fx ign =1;) = yn i=1 f(x i;) 2.to do this, nd solutions to (analytically or by following gradient) dl(fx ign i=1;) d = 0.
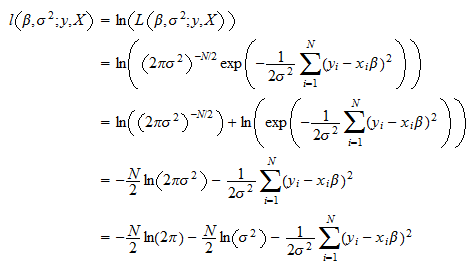
Linear Regression Maximum Likelihood Estimation

Maximum Likelihood Estimation For Linear Regression Quantstart

Comments are closed.