Simple Linear Regression Derivation The Slope And Intercept In 2 Ways The Least Squares Criterion

By gudangdomain On Nov 8, 2024 Last updated

Calculate Simple Linear Regression Equation Least Squares Peryplan I derive the least squares estimators of the slope and intercept in simple linear regression (using summation notation, and no matrices.) i assume that the. Simple linear regression derivation of the slope and intercept in 2 ways. the least squares criterion.

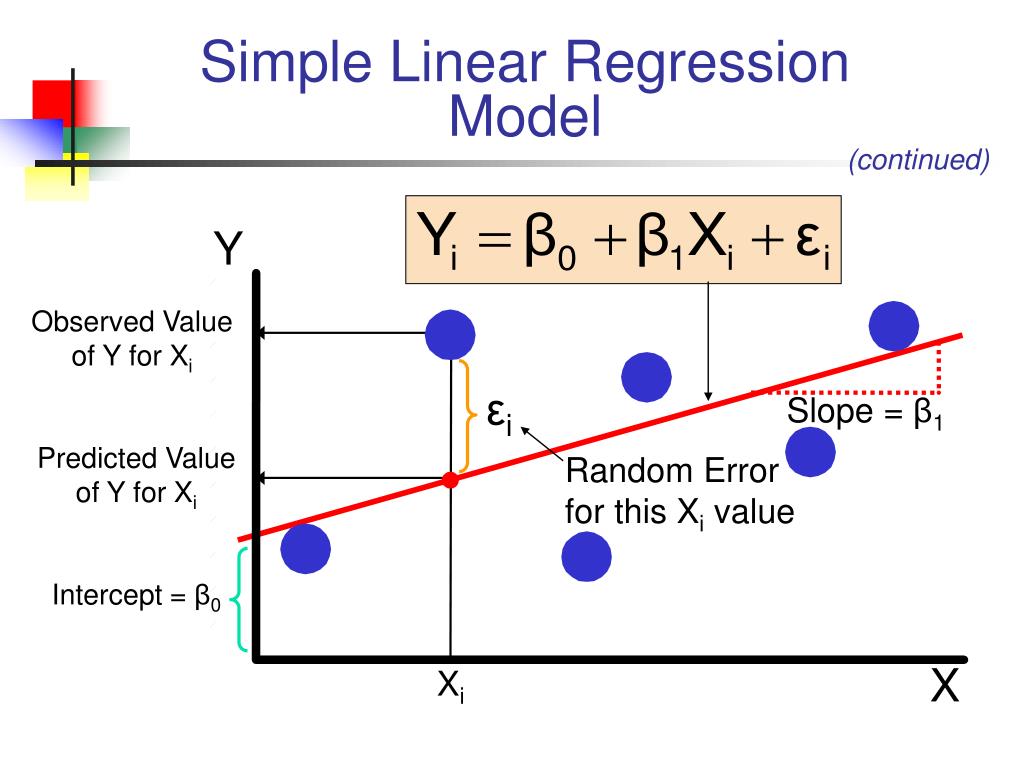
Simple Linear Regression 3 5 Standard Error Of Slope And Intercept 2.7 derivation for slope and intercept. this document contains the mathematical details for deriving the least squares estimates for slope (β1 β 1) and intercept (β0 β 0). we obtain the estimates, ^β1 β ^ 1 and ^β0 β ^ 0 by finding the values that minimize the sum of squared residuals (). ssr = n ∑ i=1[yi− ^yi]2 = [yi −(^β0. Simple linear regression least squares estimates of 0 and 1 simple linear regression involves the model y^ = yjx = 0 1x: this document derives the least squares estimates of 0 and 1. it is simply for your own information. you will not be held responsible for this derivation. the least squares estimates of 0 and 1 are: ^ 1 = ∑n i=1(xi x )(yi. Simple linear regression least squares (ls) estimation to estimate the regression coeﬃ cients β 0,β 1, here we adopt the least squares criterion: min βˆ 0,βˆ 1 s(βˆ 0,βˆ 1) def= xn i=1 (y i−(βˆ 0 βˆ 1x i | {z } yˆ i))2 the corresponding minimizers are called least squares estimators. remark. another way is to maximize the. Microsoft word 10.simple linear regression.doc. simple linear regression is the most commonly used technique for determining how one variable of interest (the response variable) is affected by changes in another variable (the explanatory variable). the terms "response" and "explanatory" mean the same thing as "dependent" and "independent.

Ppt Chapter 11 Simple Linear Regression Analysis 线性回归分析 Simple linear regression least squares (ls) estimation to estimate the regression coeﬃ cients β 0,β 1, here we adopt the least squares criterion: min βˆ 0,βˆ 1 s(βˆ 0,βˆ 1) def= xn i=1 (y i−(βˆ 0 βˆ 1x i | {z } yˆ i))2 the corresponding minimizers are called least squares estimators. remark. another way is to maximize the. Microsoft word 10.simple linear regression.doc. simple linear regression is the most commonly used technique for determining how one variable of interest (the response variable) is affected by changes in another variable (the explanatory variable). the terms "response" and "explanatory" mean the same thing as "dependent" and "independent. Give us a system of two linear equations in two unknowns. as we remember from linear algebra (or earlier), such systems have a unique solution, unless one of the equations of the system is redundant. (see exercise 2.) notice that this existence and uniqueness of a least squares estimate assumes absolutely nothing about the data generating process. 9.1. the model behind linear regression 217 0 2 4 6 8 10 0 5 10 15 x y figure 9.1: mnemonic for the simple regression model. than anova. if the truth is non linearity, regression will make inappropriate predictions, but at least regression will have a chance to detect the non linearity.

Whether you're looking for practical how-to guides, in-depth analyses, or thought-provoking discussions, we has got you covered. Our diverse range of topics ensures that there's something for everyone, from title_here. We're committed to providing you with valuable information that resonates with your interests.

SIMPLE LINEAR REGRESSION DERIVATION: THE SLOPE AND INTERCEPT IN 2 WAYS THE LEAST SQUARES CRITERION

SIMPLE LINEAR REGRESSION DERIVATION: THE SLOPE AND INTERCEPT IN 2 WAYS THE LEAST SQUARES CRITERION Deriving the least squares estimators of the slope and intercept (simple linear regression) How to Derive the Best Slope and Intercept in a Simple Linear Regression Linear Regression Using Least Squares Method - Line of Best Fit Equation Deriving the mean and variance of the least squares slope estimator in simple linear regression Video 1: Introduction to Simple Linear Regression Simple Linear Regression: Derivation of the Intercept and Slope Simple linear regression (2/5)- slope and intercept of linear regression model Introduction to residuals and least squares regression How To... Perform Simple Linear Regression by Hand Deriving OLS Slope and Intercept Formulas for Simple Regression Deriving the OLS Estimators in Simple Linear Regression Model - Part 1 Intro to Simple Linear Regression | Slope, y-intercept, R-square 14.2 Simple Linear Regression Interpreting Slope and Y Intercept of a Regression LIne Linear Regression #2 | Interpreting the slope and intercept coefficients Simple Linear Regression Derivation of OLS Estimators Simple Linear Regression: The Least Squares Regression Line Simple Linear Regression Using Least Squares Estimators Ordinary Least Squares regression or Linear regression

Conclusion

Taking everything into consideration, it can be concluded that this particular article offers informative data with respect to Simple Linear Regression Derivation The Slope And Intercept In 2 Ways The Least Squares Criterion. Throughout the article, the reporter manifests remarkable understanding pertaining to the theme. In particular, the analysis of this detail stands out as a major point. Besides, the piece performs admirably in simplifying complex concepts in an accessible manner. Moreover, the author shares applicable examples that heighten the understanding. A further characteristic that differentiates this write-up is the in-depth research of numerous aspects related to Simple Linear Regression Derivation The Slope And Intercept In 2 Ways The Least Squares Criterion. The creators rigorous method secures that spectators obtain a comprehensive insight of the subject matter. Thank you for reading the post. If theres anything else youd like to know, please feel free to touch base using any social network. I await your input. In bringing things to a close, for further insights, here are various relevant texts that are beneficial:Hope you find them interesting!