Shoelace Theorem With 2 Amc 12 Examples

Shoelace Theorem With 2 Amc 12 Examples Youtube In this video i demonstrate the basic underpinnings of the application of shoelace theorem. i only currently have an operational level understanding of this. Solution 3 (shoelace theorem) the consecutive vertices of the shaded figure are and by the shoelace theorem, the area is ~taco12 ~i am da king solution 4 (pick's theorem) we have lattice points in the interior and lattice points on the boundary. by pick's theorem, the area of the shaded figure is ~danprathab video solution by interstigation.
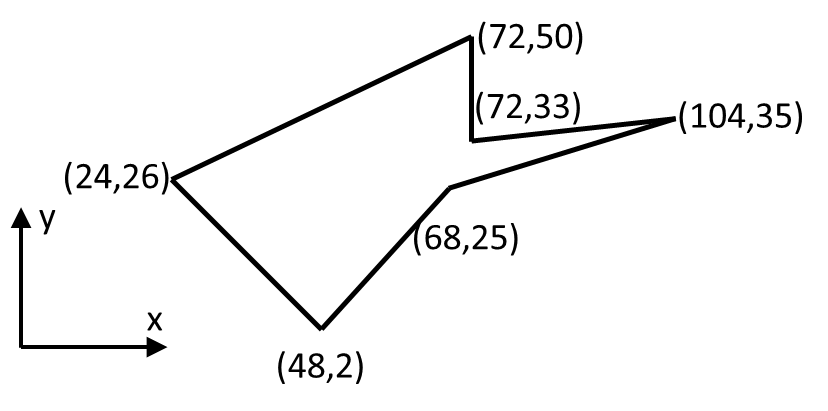
Lesson 109 Shoelace Method Math Showme Solution 2 (shoelace) let the point of intersection be , with coordinates . then, is cut into and . since the areas are equal, we can use shoelace theorem to find the area. this gives . the line going through is . since is on , we can substitute this in, giving . solving for gives . plugging this back into the line equation gives , for a final. Then, applying the shoelace theorem on and we get hence as claimed. ~shreyj proof 2. let be the set of points belonging to the polygon. we have that where . the volume form is an exact form since , where using this substitution, we have next, we use the theorem of stokes to obtain we can write , where is the line segment from to . Solution 2 shoelace theorem. we know lines and intersect at , so we can solve for that point: because we have: thus we have . we know that the area of the triangle is , so by shoelace theorem we have: thus we have two options: or. now we must just find a point that satisfies is positive. doing some guess and check yields, from the second. Solution 2. use the shoelace theorem. let the center of the first circle of radius 1 be at . draw the trapezoid and using the pythagorean theorem, we get that so the center of the second circle of radius 2 is at . draw the trapezoid and using the pythagorean theorem, we get that so the center of the third circle of radius 3 is at .
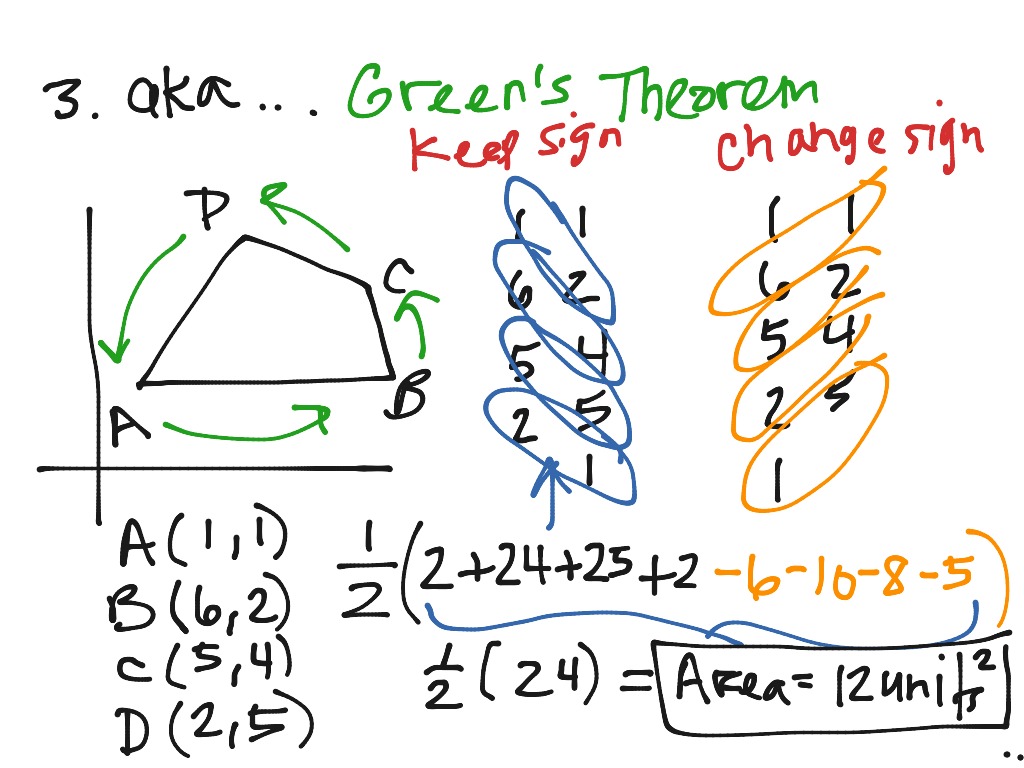
Quick And Easy Way To Calculate The Area Of Any Polygon The Shoelace Solution 2 shoelace theorem. we know lines and intersect at , so we can solve for that point: because we have: thus we have . we know that the area of the triangle is , so by shoelace theorem we have: thus we have two options: or. now we must just find a point that satisfies is positive. doing some guess and check yields, from the second. Solution 2. use the shoelace theorem. let the center of the first circle of radius 1 be at . draw the trapezoid and using the pythagorean theorem, we get that so the center of the second circle of radius 2 is at . draw the trapezoid and using the pythagorean theorem, we get that so the center of the third circle of radius 3 is at . The shoelace theorem is a method for calculating the area of a simple (non self intersecting) polygon in the plane given only the coordinates of its vertices. for example: this polygon has area 12. the shoelace theorem says we can calculate the area by writing the coordinates in clockwise order in a column, repeat the first pair, then multiply. Amc 12 preparation berkeley math circle 1.2 combinatorics c1. (omo winter 2013) david has a collection of 40 rocks, 30 stones, 20 minerals and (for example, x 2.

Learning The Shoelace Method With An Amc Problem Youtube The shoelace theorem is a method for calculating the area of a simple (non self intersecting) polygon in the plane given only the coordinates of its vertices. for example: this polygon has area 12. the shoelace theorem says we can calculate the area by writing the coordinates in clockwise order in a column, repeat the first pair, then multiply. Amc 12 preparation berkeley math circle 1.2 combinatorics c1. (omo winter 2013) david has a collection of 40 rocks, 30 stones, 20 minerals and (for example, x 2.

An Elegant Proof Of The Shoelace Method Youtube

Higher Dimensional Shoelace Theorems

Comments are closed.