Reference Angles And Evaluating Trig Functions Bs Education Studocu

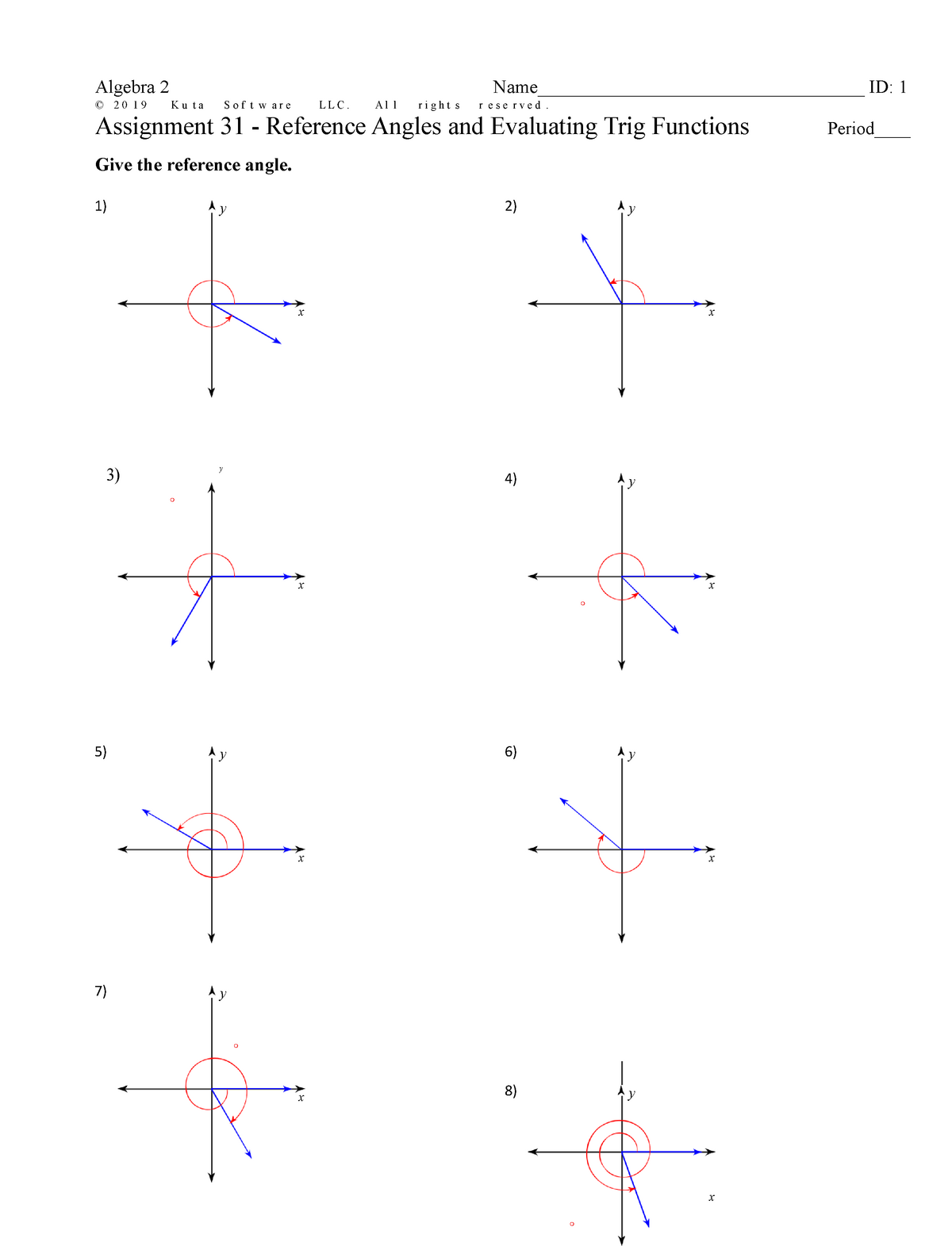
Reference Angles And Evaluating Trig Functions Bs Education Studocu Reference angle and evaluating trig function practice sheet algebra 20 19 id: ku ta sof are llc. al right ese rved assignment 31 reference angles and. Bs education (educ 95) b. reference: department of education (2014). mathematics learner’s material. reference angles and evaluating trig functions; english.

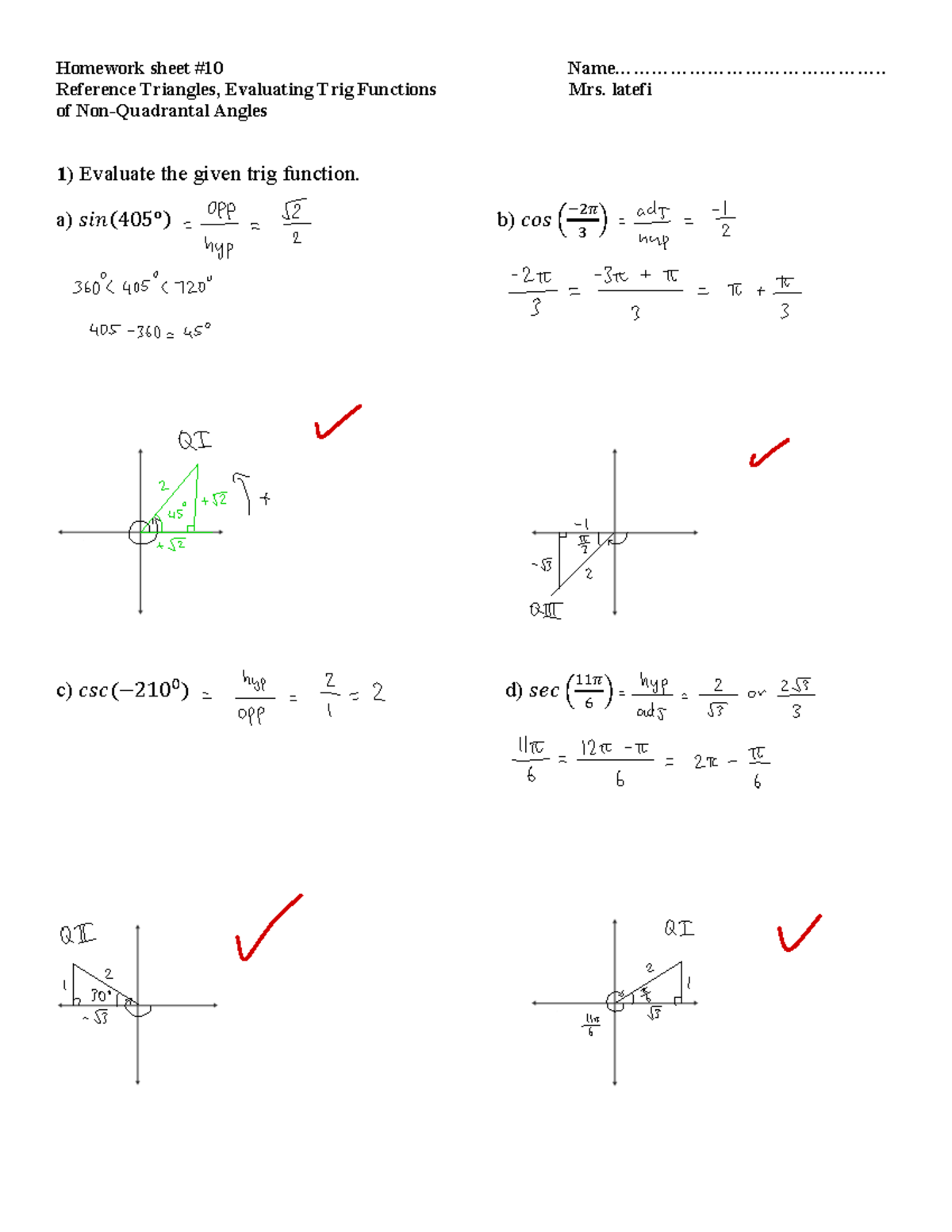
Hw 10 Hw Key For College Trigonometry Reference Triangles Reference triangles, evaluating trig functions mrs. latefi of non quadrantal angles evaluate the given trig function. a) 𝑠𝑖𝑛(405°) b) 𝑐𝑜𝑠 ( −2𝜋 3 ) c) 𝑐𝑠𝑐(−210 0 ) d) 𝑠𝑒𝑐 ( 11𝜋 6 ) p = e i = hyp368%405°. 150° is located in the second quadrant. the angle it makes with the x axis is 180° − 150° = 30°, so the reference angle is 30°.this tells us that 150° has the same sine and cosine values as 30°, except for the sign. we know that. cos (3 0 ∘) = 3 2 a n d sin (3 0 ∘) = 1 2. To find the value of a trigonometric function of any angle t: determine the function value for the associated reference angle t'. depending on the quadrant in which t lies, the answer will be either be or . how to evaluate trig functions using reference angles? find the reference angle for the given angle. In this video, we will learn how to find the reference angle and principal angle of an angle in standard position, and we will learn how to use these to evaluate trigonometric functions. to do this, we first need to recall how we evaluate the trigonometric functions. that’s the sine of an angle and the cosine of an angle.

Evaluating Trig Functions Of Any Angle Part 2 Mth 121 Studocu To find the value of a trigonometric function of any angle t: determine the function value for the associated reference angle t'. depending on the quadrant in which t lies, the answer will be either be or . how to evaluate trig functions using reference angles? find the reference angle for the given angle. In this video, we will learn how to find the reference angle and principal angle of an angle in standard position, and we will learn how to use these to evaluate trigonometric functions. to do this, we first need to recall how we evaluate the trigonometric functions. that’s the sine of an angle and the cosine of an angle. Let me teach you what a reference angle is and how we can use them to make evaluating trig functions a lot of easier! it also helps us not have to memorize a. If one angle is an reference angle of another, the trigonometric functions of these two angles have the same values in magnitude, and we just need to pay attention to their signs based on the quadrant that the terminal side of the angle lies in. for example, 30° is the reference angle of 210° with sine values sin(30°)= and sin(210°)=.