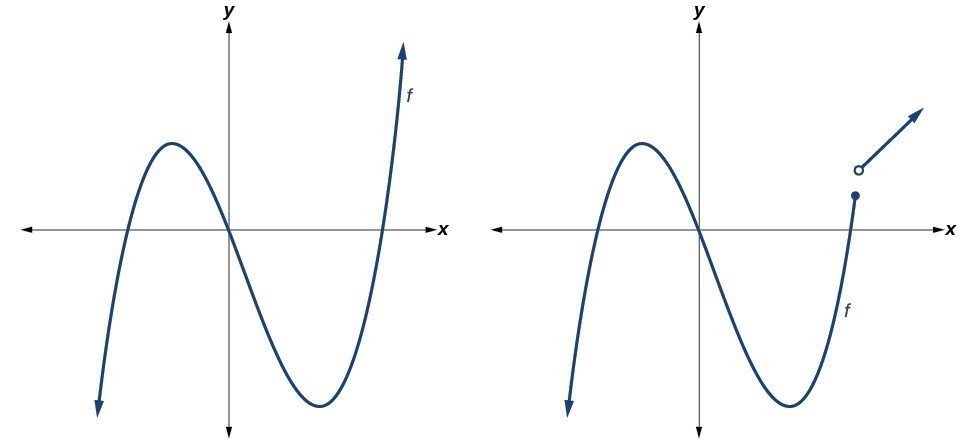
Recognize Characteristics Of Graphs Of Polynomial Functions College Recognizing characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. Recognize characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. figure 1 shows a graph that.
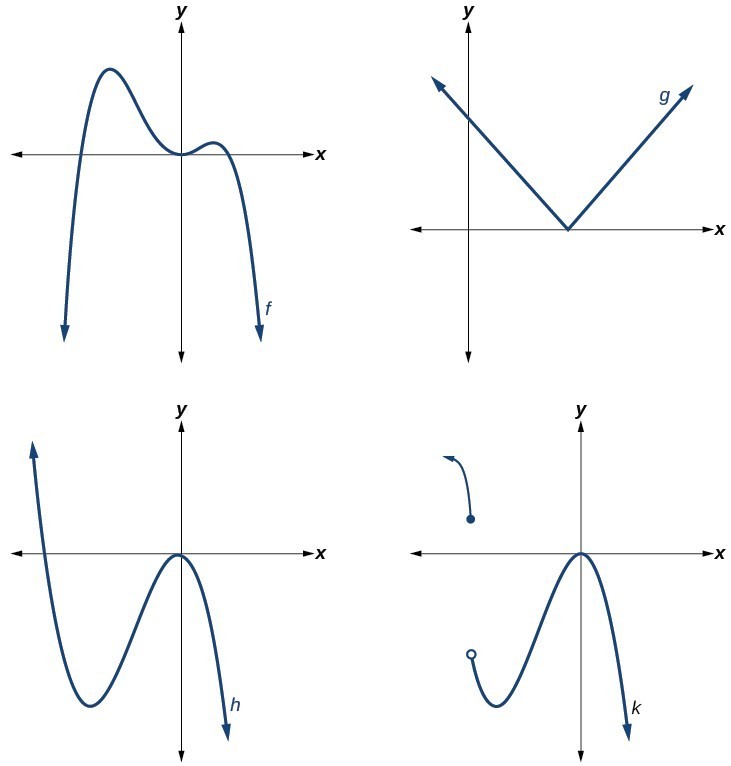
Recognize Characteristics Of Graphs Of Polynomial Functions College Recognizing characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n − 1 turning points. Figure 5.4.9 5.4. 9: graph of a polynomial function with degree 5. solution. the polynomial function is of degree n n. the sum of the multiplicities must be n n. starting from the left, the first zero occurs at x = −3 x = − 3. the graph touches the x axis, so the multiplicity of the zero must be even. For any polynomial, the graph of the polynomial will match the end behavior of the term of highest degree. as an example, we compare the outputs of a degree 2 2 polynomial and a degree 5 5 polynomial in the following table. x. f (x)=2x^2 2x 4 f (x) = 2x2 −2x 4. g (x)=x^5 2x^3 12x 3 g(x) = x5 2x3 −12x 3. 1 1. 4 4.
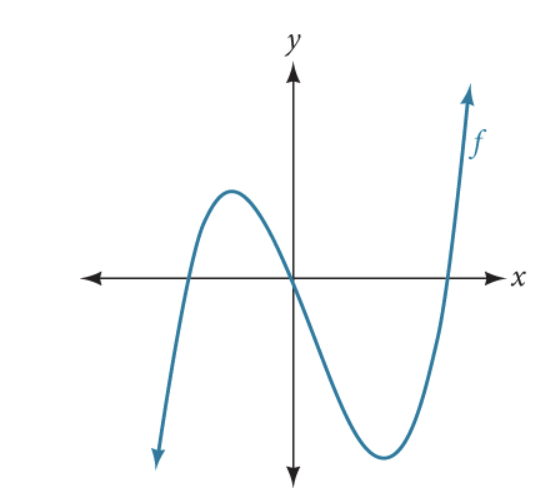
College Algebra Graphs Of Polynomial Functions Oertx Figure 5.4.9 5.4. 9: graph of a polynomial function with degree 5. solution. the polynomial function is of degree n n. the sum of the multiplicities must be n n. starting from the left, the first zero occurs at x = −3 x = − 3. the graph touches the x axis, so the multiplicity of the zero must be even. For any polynomial, the graph of the polynomial will match the end behavior of the term of highest degree. as an example, we compare the outputs of a degree 2 2 polynomial and a degree 5 5 polynomial in the following table. x. f (x)=2x^2 2x 4 f (x) = 2x2 −2x 4. g (x)=x^5 2x^3 12x 3 g(x) = x5 2x3 −12x 3. 1 1. 4 4. The graph of a polynomial will touch and bounce off the x axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n – 1 turning points. Recognize characteristics of graphs of polynomial functions. use factoring to find zeros of polynomial functions. identify zeros and their multiplicities. determine end behavior. understand the relationship between degree and turning points. graph polynomial functions. use the intermediate value theorem.
Comments are closed.