Question Video Using The Cosine Rule To Find An Unknown Angle In A

Question Video Using The Cosine Rule To Find An Unknown Angle In A Find the measure of angle 𝐴 to one decimal place. in this question, we’re given the lengths of all three sides of our triangle. and we need to calculate the measure of one of the angles. we can do this using the law of cosines. this states that 𝑎 squared is equal to 𝑏 squared plus 𝑐 squared minus two 𝑏𝑐 multiplied by the cos. Evaluating each of these terms gives 𝑐 squared is equal to 100 plus 169 minus 52. this simplifies to 𝑐 squared is equal to 217. next, in order to find the value of 𝑐, we need to take the square root of both sides of this equation. so 𝑐 is equal to the square root of 217. and as a decimal, this is 14.730919.

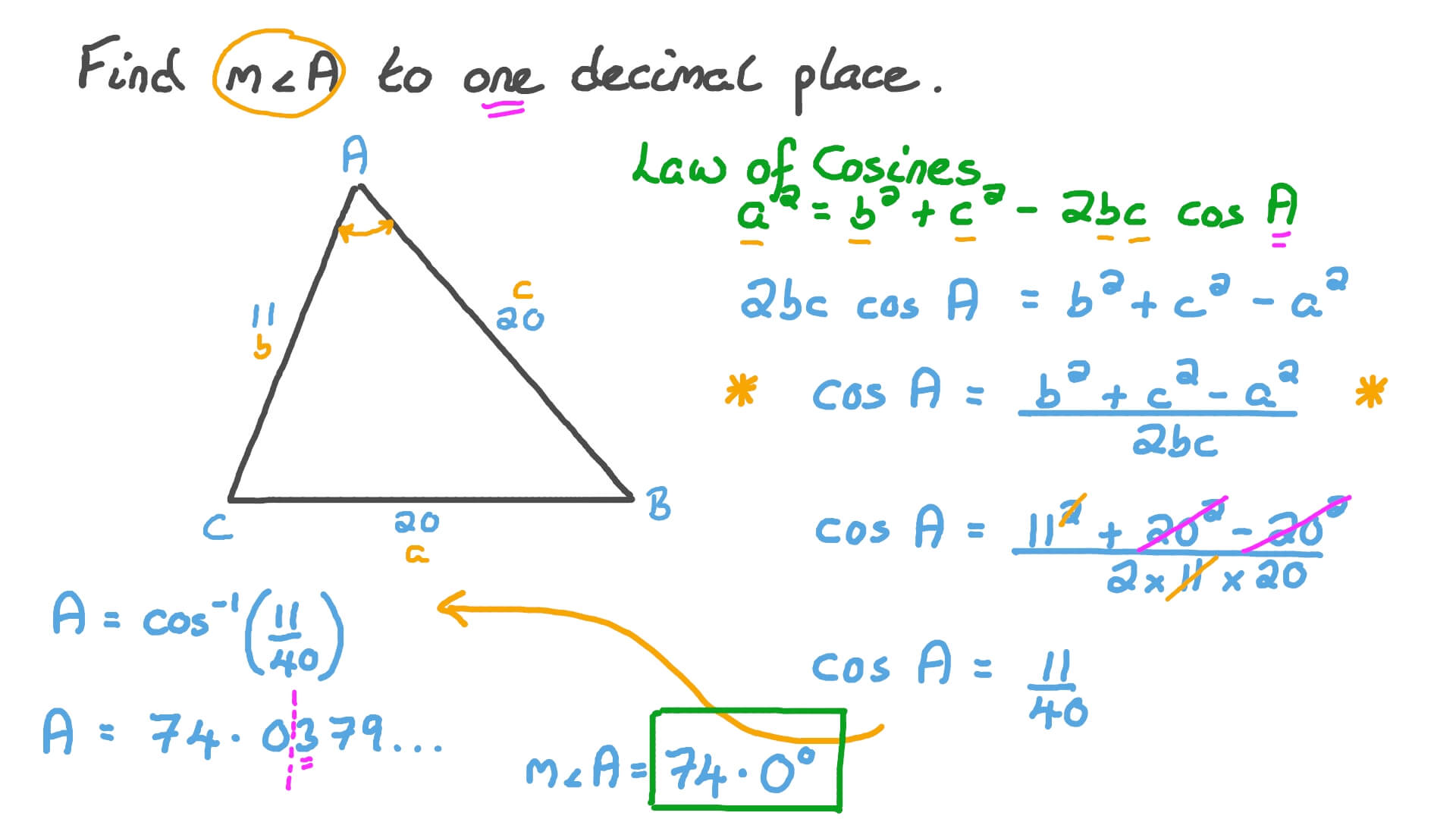
Question Video Using The Cosine Rule To Find An Unknown Angle In A Discover how to use the cosine rule to find the unknown angle of a triangle in this straightforward video. gain confidence with step by step guidance and pra. Using the cosine rule to find an unknown angle. Video transcript. find the size of angle 𝐴, in degrees, of the triangle shown. looking at this triangle, we see that all three side lengths are given to us, and we want to solve for this unknown angle here. given this information, we can use the cosine rule to solve for this angle 𝐴. Example 3: find the missing side using the cosine rule. find the length of z for triangle xyz. write your answer to a suitable degree of accuracy. label each angle (a, b, c) and each side (a, b, c) of the triangle. show step. in order to find the length of z, we need to know the opposite angle at z.

Question Video Using Cosine Role To Calculate An Unknown Angle Of A Video transcript. find the size of angle 𝐴, in degrees, of the triangle shown. looking at this triangle, we see that all three side lengths are given to us, and we want to solve for this unknown angle here. given this information, we can use the cosine rule to solve for this angle 𝐴. Example 3: find the missing side using the cosine rule. find the length of z for triangle xyz. write your answer to a suitable degree of accuracy. label each angle (a, b, c) and each side (a, b, c) of the triangle. show step. in order to find the length of z, we need to know the opposite angle at z. Course: precalculus > unit 2. lesson 5: law of cosines. solving for a side with the law of cosines. solving for an angle with the law of cosines. solve triangles using the law of cosines. proof of the law of cosines. 1. find the missing side length of a triangle. the two known side lengths are 20 and 17 cm long. the angle between these two sides is 68 degrees. since you know two side lengths, and the angle between them, you can use the cosine rule. set up the formula: .