Pythagorean Theorem Six Proofs

How To Use The Pythagorean Theorem Step By Step Examples And Practice Pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see two squares inside the. This video illustrates six different proofs for the pythagorean theorem as six little beautiful visual puzzles.originally created for the "1 minuto" film fes.

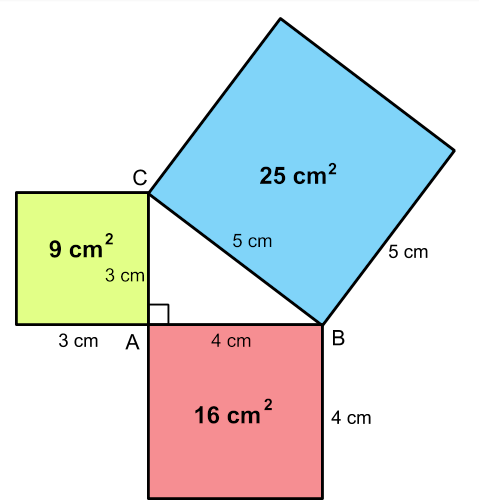
Pythagorean Theorem Six Proofs Mathslinks The pythagorean theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. so if a a and b b are the lengths of the legs, and c c is the length of the hypotenuse, then a^2 b^2=c^2 a2 b2 = c2. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem. Some popular dissection proofs of the pythagorean theorem such as proof #36 on cut the knot demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. i have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra.

Pythagorean Theorem And Its Various Proofs Some popular dissection proofs of the pythagorean theorem such as proof #36 on cut the knot demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. i have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. The pythagorean theorem is a relation in a right angled triangle. the rule states that a2 b2 = c2 , in which a and b are the opposite and the adjacent sides, the 2 sides which make the right angle, and c representing the hypotenuse, the longest side of the triangle. so if you have a = 6 and b = 8, c would equal to (62 82)1 2, (x1 2 meaning. This video illustrates six different proofs for the pythagorean theorem as six little beautiful visual puzzles. 27 december 2018 edit: 27 december 2018 user submitted, thanks to scott smith.

Proofs Of Pythagoras Theorem The pythagorean theorem is a relation in a right angled triangle. the rule states that a2 b2 = c2 , in which a and b are the opposite and the adjacent sides, the 2 sides which make the right angle, and c representing the hypotenuse, the longest side of the triangle. so if you have a = 6 and b = 8, c would equal to (62 82)1 2, (x1 2 meaning. This video illustrates six different proofs for the pythagorean theorem as six little beautiful visual puzzles. 27 december 2018 edit: 27 december 2018 user submitted, thanks to scott smith.
The Pythagorean Theorem Math Tutor Free Math For All

Comments are closed.