Pythagorean Theorem Proof Geometry

How To Prove The Pythagorean Theorem 10 Steps With Pictures The pythagorean theorem provides an equation to calculate the longer side of a right triangle by summing the squares of the other two sides. it is often phrased as. a2 b2 c2. in this equation, a. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra.
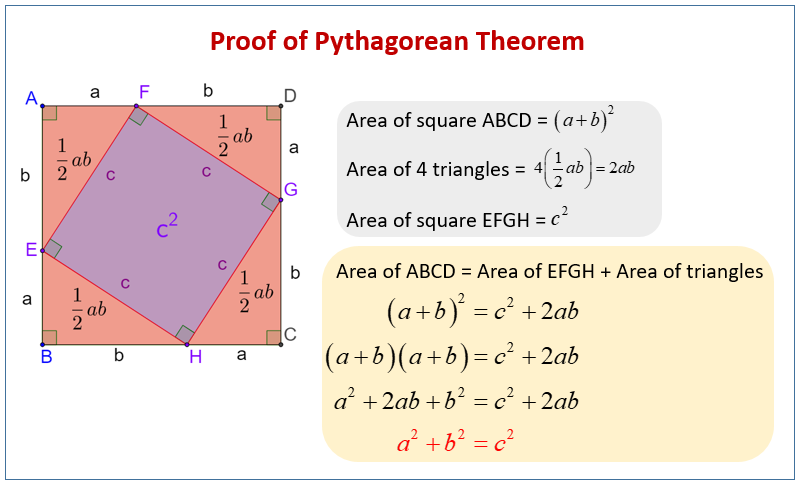
Proving The Pythagorean Theorem Math Liberty Proof by rearrangement. pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see. In mathematics, the pythagorean theorem or pythagoras' theorem is a fundamental relation in euclidean geometry between the three sides of a right triangle. it states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. It is located directly opposite the right angle of the triangle. most importantly, it is the quantity that is isolated by itself in the pythagorean theorem (equation 7.4.1). always isolate the quantity representing the hypotenuse on one side of the equation. the "legs" go on the other side of the equation. Some popular dissection proofs of the pythagorean theorem such as proof #36 on cut the knot demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. i have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same.
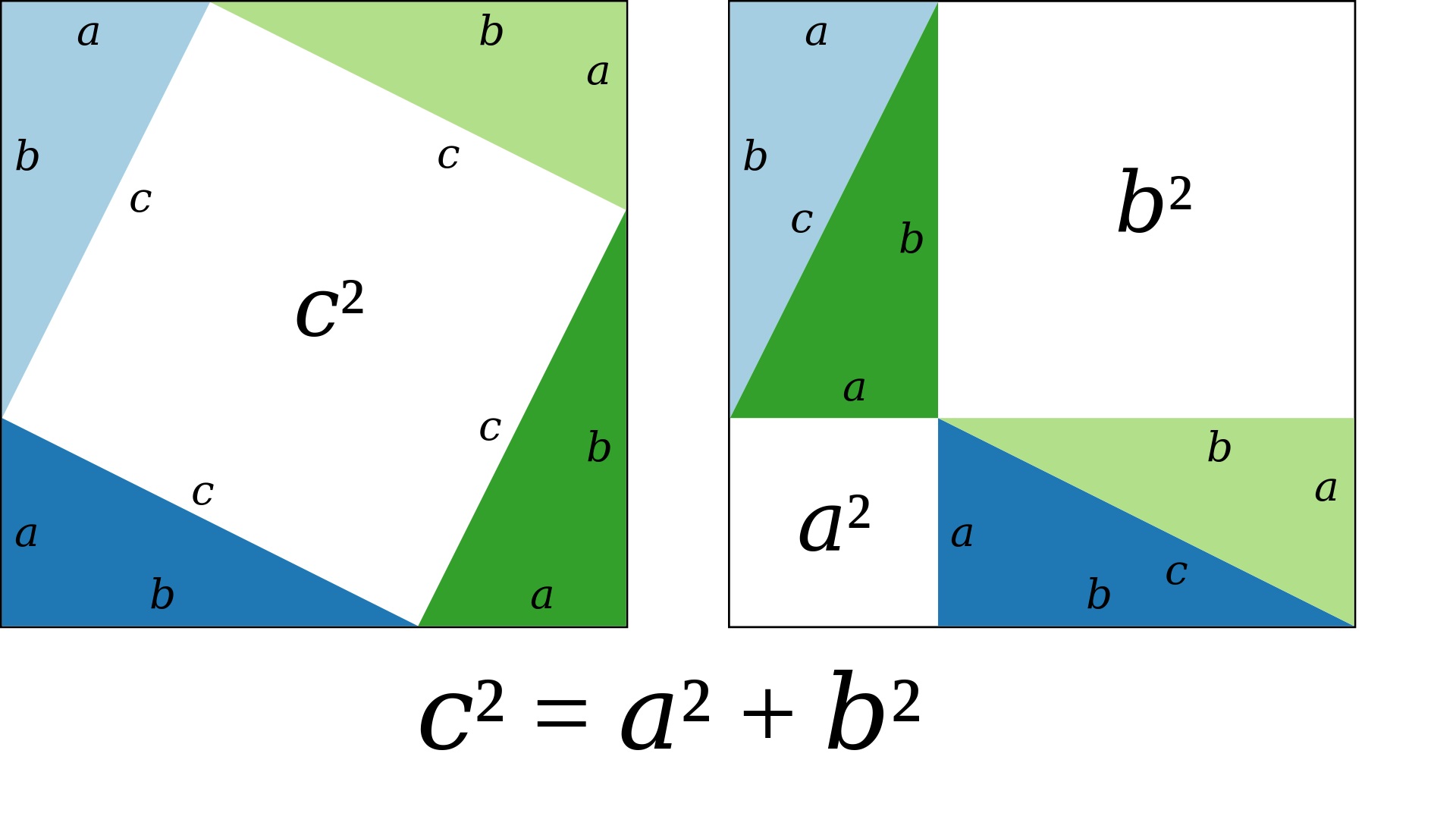
Pythagorean Theorem Proof It is located directly opposite the right angle of the triangle. most importantly, it is the quantity that is isolated by itself in the pythagorean theorem (equation 7.4.1). always isolate the quantity representing the hypotenuse on one side of the equation. the "legs" go on the other side of the equation. Some popular dissection proofs of the pythagorean theorem such as proof #36 on cut the knot demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. i have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem. There are many unique proofs (more than 350) of the pythagorean theorem, both algebraic and geometric. the proof presented below is helpful for its clarity and is known as a proof by rearrangement. in a right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse.
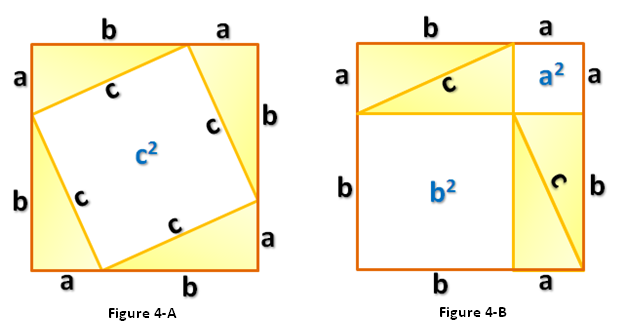
The Algebraic And Geometric Proofs Of Pythagorean Theorem Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem. There are many unique proofs (more than 350) of the pythagorean theorem, both algebraic and geometric. the proof presented below is helpful for its clarity and is known as a proof by rearrangement. in a right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse.

How To Prove Pythagoras Theorem Using Geometry And Algebra Quick

Comments are closed.