Pythagorean Theorem Euclid Proof And Formula Right Triangle Basic

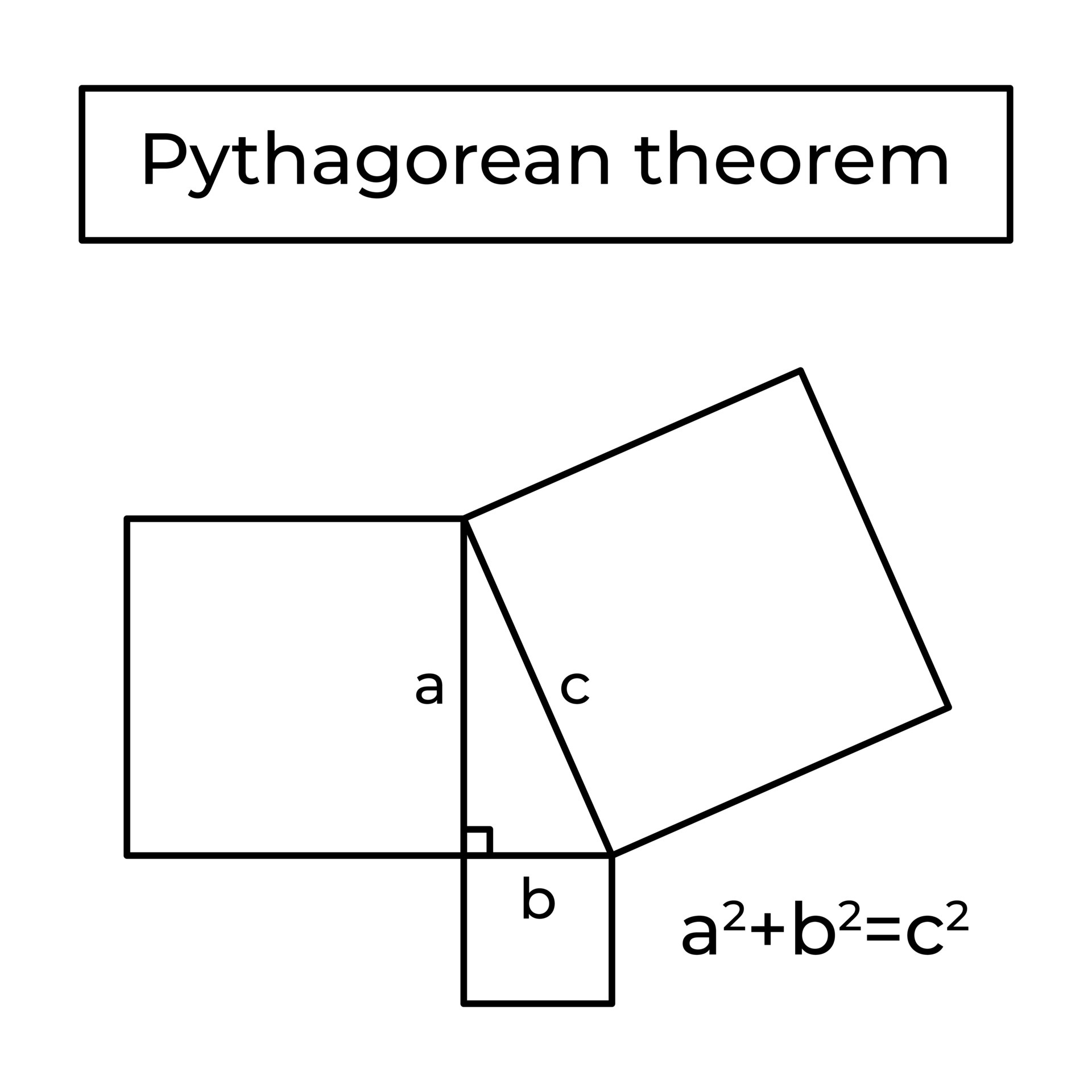
Pythagorean Theorem Euclid Proof And Formula Right Triangle Basic For the comparison and reference sake we'll have on this page the proof of the pythagorean theorem as it is given in elements i.47, see . in right angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle. let abc be a right angled triangle having the angle bac right. Explain the steps involved in finding the sides of a right triangle using pythagoras theorem. step 1: to find the unknown sides of a right triangle, plug the known values in the pythagoras theorem formula. step 2: simplify the equation to find the unknown side. step 3: solve the equation for the unknown side. q8.

Pythagorean Theorem Euclid Proof And Formula Right Triangle Basic Interior angle Δθ = θ 1 −θ 2. the pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that where is the angle between sides and . [45] when is radians or 90°, then , and the formula reduces to the usual pythagorean theorem. Proof by rearrangement. pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem.

Euclid S Elements Pythagorean Theorem Mathematical Proof Right Triangle What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem. The hypotenuse is the longest side of the right triangle. it is located directly opposite the right angle of the triangle. most importantly, it is the quantity that is isolated by itself in the pythagorean theorem (equation 7.4.1). always isolate the quantity representing the hypotenuse on one side of the equation. A great many different proofs and extensions of the pythagorean theorem have been invented. taking extensions first, euclid himself showed in a theorem praised in antiquity that any symmetrical regular figures drawn on the sides of a right triangle satisfy the pythagorean relationship: the figure drawn on the hypotenuse has an area equal to the sum of the areas of the figures drawn on the legs.