Pythagoras Theorem Statement Formula Proof And Examples
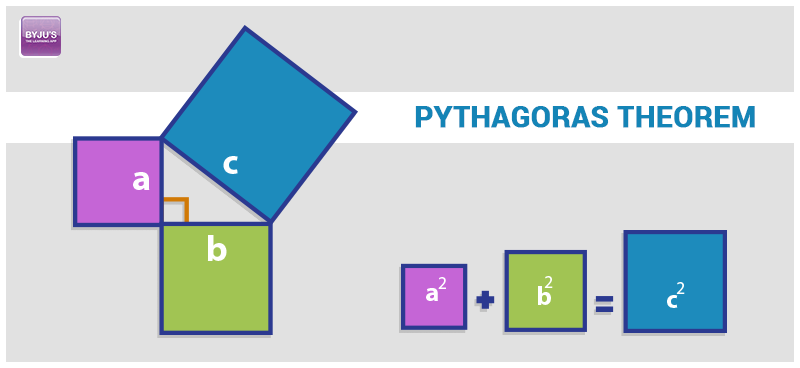
Pythagoras Theorem Statement Formula Proof And Examples The formula and proof of this theorem are explained here with examples. pythagoras theorem is basically used to find the length of an unknown side and the angle of a triangle. by this theorem, we can derive the base, perpendicular and hypotenuse formulas. let us learn the mathematics of the pythagorean theorem in detail here. Example 1: the hypotenuse of a right angled triangle is 16 units and one of the sides of the triangle is 8 units. find the measure of the third side using the pythagoras theorem formula. solution: given: hypotenuse = 16 units. let us consider the given side of a triangle as the perpendicular height = 8 units.

How To Prove The Pythagorean Theorem 10 Steps With Pictures Pythagoras theorem formula is ac2 = ab2 bc2, where ab is the perpendicular side, bc is the base, and ac is the hypotenuse side. the pythagoras equation is applied to any right angled triangle, a triangle that has one of its angles equal to 90°. pythagoras formula. the three sides of the right angled triangle are called the pythagoras triplets. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. The sum of the smaller squares (orange and yellow) is equal to the largest square (blue). the pythagorean theorem relates the three sides in a right triangle. to be specific, relating the two legs and the hypotenuse, the longest side. the pythagorean theorem can be summarized in a short and compact equation as shown below. It is called "pythagoras' theorem" and can be written in one short equation: a 2 b 2 = c 2. note: c is the longest side of the triangle; a and b are the other two sides; definition. the longest side of the triangle is called the "hypotenuse", so the formal definition is:.
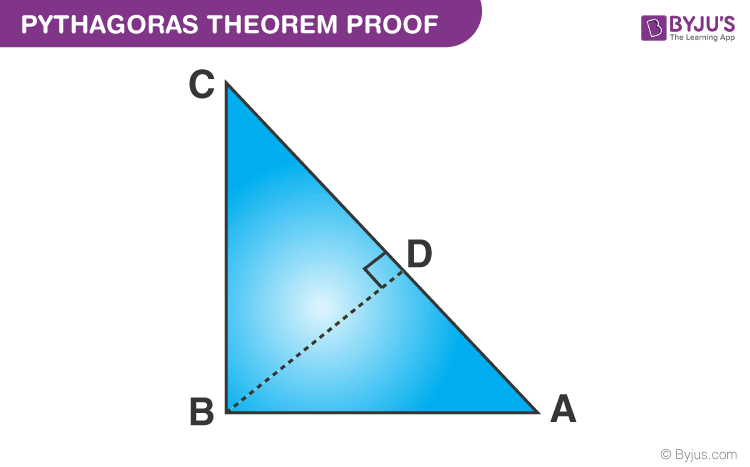
Pythagoras Theorem Formula Proof Examples Applications The sum of the smaller squares (orange and yellow) is equal to the largest square (blue). the pythagorean theorem relates the three sides in a right triangle. to be specific, relating the two legs and the hypotenuse, the longest side. the pythagorean theorem can be summarized in a short and compact equation as shown below. It is called "pythagoras' theorem" and can be written in one short equation: a 2 b 2 = c 2. note: c is the longest side of the triangle; a and b are the other two sides; definition. the longest side of the triangle is called the "hypotenuse", so the formal definition is:. Pythagoras theorem equations • b 2 = c 2 a 2 and a 2 = c 2 b 2 • c = √ (a 2 b 2) • b = √ (c 2 a 2) and a = √ (c 2 b 2) pythagoras theorem formulas. the pythagoras theorem formulas states that in a right angled triangle abc, the square of the hypotenuse ac is equal to the sum of the squares of the other two sides ab and bc. The pythagorean theorem shows the relationship between the sides of a right triangle. it states that for a right triangle, the sum of the areas of the squares formed by the legs of the triangle equals the area of the square formed by the triangle's hypotenuse. this is expressed as: a 2 b 2 = c 2. where a and b are the legs of a right triangle.

Proving The Pythagorean Theorem Youtube Pythagoras theorem equations • b 2 = c 2 a 2 and a 2 = c 2 b 2 • c = √ (a 2 b 2) • b = √ (c 2 a 2) and a = √ (c 2 b 2) pythagoras theorem formulas. the pythagoras theorem formulas states that in a right angled triangle abc, the square of the hypotenuse ac is equal to the sum of the squares of the other two sides ab and bc. The pythagorean theorem shows the relationship between the sides of a right triangle. it states that for a right triangle, the sum of the areas of the squares formed by the legs of the triangle equals the area of the square formed by the triangle's hypotenuse. this is expressed as: a 2 b 2 = c 2. where a and b are the legs of a right triangle.

Comments are closed.