Prove That Root 5 Is Irrational Number Edurev Class 10 Question
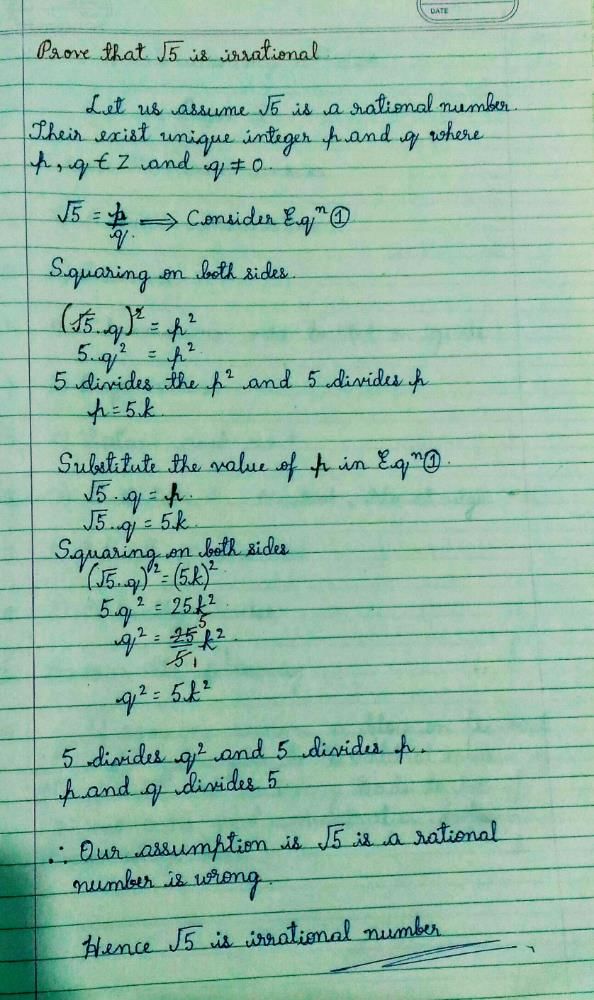
Prove That Root 5 Is Irrational Number Edurev Class 10 Question The question and answers have been prepared according to the class 10 exam syllabus. information about prove that root 5 is irrational number? covers all topics & solutions for class 10 2024 exam. find important definitions, questions, meanings, examples, exercises and tests below for prove that root 5 is irrational number?. Verified answer. prove that root 5 is irrational? let us assume that √5 is a rational number. we know that the rational numbers are in the form of p q form where p,q are intezers. so, √5 = p q. p = √5q. we know that 'p' is a rational number. so √5 q must be rational since it equals to p. but it doesnt occurs with √5 since its not an.

Prove That Root 5 Is Irrational Number Edurev Class 10 Question Step 1 let us assume that √5 is a rational number. this means that we can write √5 as a ratio of two integers a and b such that: √5 = a b step 2 we can square both sides of the equation to get: 5 = (a b)^2 step 3 we can multiply both sides of the equation by b^2 to get: 5b^2 = a^2 step 4 since a^2 is a multiple of 5, a must be a multiple. Irrational numbers | prove that root 5 is irrational number | irrational numbers for class 10🔥ex1.1 class10 maths new session 2023 24🔥| real number class. Transcript. ex 1.2, 1 prove that √5 is irrational. we have to prove √5 is irrational let us assume the opposite, i.e., √5 is rational hence, √5 can be written in the form 𝑎 𝑏 where a and b (b≠ 0) are co prime (no common factor other than 1) hence, √𝟓 = 𝒂 𝒃 √5 b = a squaring both sides (√5b)2 = a2 5b2 = a2 𝒂^𝟐 𝟓 = b2 hence, 5 divides a2 so, 5 shall divide. This question can be proved with the help of the contradiction method. let's assume that √5 is a rational number. if √5 is rational, that means it can be written in the form of a b, where a and b integers that have no common factor other than 1 and b ≠ 0. i.e., a and b are coprime numbers. √5 1 = a b. √5b = a. squaring both sides,.

Prove That Root 5 Is Irrational Edurev Class 10 Question Transcript. ex 1.2, 1 prove that √5 is irrational. we have to prove √5 is irrational let us assume the opposite, i.e., √5 is rational hence, √5 can be written in the form 𝑎 𝑏 where a and b (b≠ 0) are co prime (no common factor other than 1) hence, √𝟓 = 𝒂 𝒃 √5 b = a squaring both sides (√5b)2 = a2 5b2 = a2 𝒂^𝟐 𝟓 = b2 hence, 5 divides a2 so, 5 shall divide. This question can be proved with the help of the contradiction method. let's assume that √5 is a rational number. if √5 is rational, that means it can be written in the form of a b, where a and b integers that have no common factor other than 1 and b ≠ 0. i.e., a and b are coprime numbers. √5 1 = a b. √5b = a. squaring both sides,. Real numbers class 10| how to prove root 5 an irrational number| proof of root5 an irrational number@class10studyhubreal numbers class 10,real numbers class. Yes, 2 times the square root of 5 is an irrational number as 2 × √5 = 2 × 2.23606797749979 = 4.472135954999579 a rational number multiplied with an irrational number is irrational. 2 is a rational number which is multiplied with root 5 which is irrational. thus, 2 times the square root of 5 is irrational.

Prove That Root 5 Is Irrational Number Edurev Class 10 Question Real numbers class 10| how to prove root 5 an irrational number| proof of root5 an irrational number@class10studyhubreal numbers class 10,real numbers class. Yes, 2 times the square root of 5 is an irrational number as 2 × √5 = 2 × 2.23606797749979 = 4.472135954999579 a rational number multiplied with an irrational number is irrational. 2 is a rational number which is multiplied with root 5 which is irrational. thus, 2 times the square root of 5 is irrational.

Comments are closed.