Prove That 32√5 Is Irrational Irrational Numbers
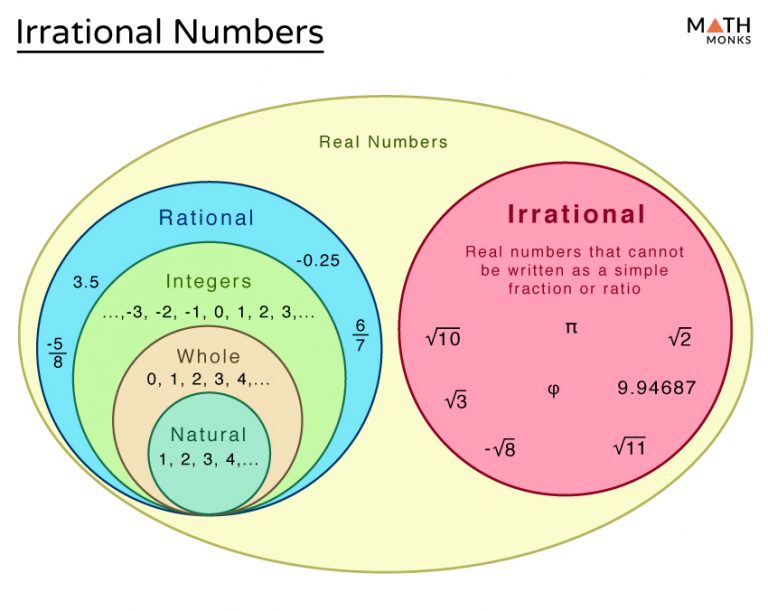
5 Examples Of Irrational Numbers An irrational number is a real number that cannot be expressed as a ratio of two integers. in simpler terms, it cannot be written in the form p q, where p and q are integers, and q is not equal to zero. the decimal representation of an irrational number neither terminates nor repeats. Course: algebra 1 > unit 15. lesson 3: proofs concerning irrational numbers. proof: √2 is irrational. proof: square roots of prime numbers are irrational. proof: there's an irrational number between any two rational numbers. irrational numbers: faq.

Irrational Numbers Gcse Maths Steps Examples Worksheet Theorem: prove that the square root of any irrational number is irrational. proof: => suppose not. the square root of any irrational number is rational. => let m be some irrational number. it follows that m−−√ is rational. => by definition of a rational number, there are two positive integers p and q such that m−−√ = q p. => m = q2 p2. Proof: √2 is irrational. proof: square roots of prime numbers are irrational. proof: there's an irrational number between any two rational numbers. Q. given that 2 is irrational, prove that 5 3 2 is an irrational number. q. prove that √5 is an irrational number. q. prove that √2 is on irrational number and also prove that 3 5√2 is irrational number. view more. But √4 = 2 is rational, and √9 = 3 is rational so not all roots are irrational. note on multiplying irrational numbers. have a look at this: π × π = π 2 is known to be irrational; but √2 × √2 = 2 is rational; so be careful multiplying irrational numbers might result in a rational number!.

List Of Irrational Numbers Q. given that 2 is irrational, prove that 5 3 2 is an irrational number. q. prove that √5 is an irrational number. q. prove that √2 is on irrational number and also prove that 3 5√2 is irrational number. view more. But √4 = 2 is rational, and √9 = 3 is rational so not all roots are irrational. note on multiplying irrational numbers. have a look at this: π × π = π 2 is known to be irrational; but √2 × √2 = 2 is rational; so be careful multiplying irrational numbers might result in a rational number!. The value obtained for the root of 5 does not terminate and keeps extending further after the decimal point. this satisfies the condition of √5 being an irrational number. hence, √5 is an irrational number. the square root of 5 is commonly also called "root 5". the root of a number "n" is represented as √n. Transcript. ex 1.2, 1 prove that √5 is irrational. we have to prove √5 is irrational let us assume the opposite, i.e., √5 is rational hence, √5 can be written in the form 𝑎 𝑏 where a and b (b≠ 0) are co prime (no common factor other than 1) hence, √𝟓 = 𝒂 𝒃 √5 b = a squaring both sides (√5b)2 = a2 5b2 = a2 𝒂^𝟐 𝟓 = b2 hence, 5 divides a2 so, 5 shall divide.

Irrational Numbers Examples Format Pdf The value obtained for the root of 5 does not terminate and keeps extending further after the decimal point. this satisfies the condition of √5 being an irrational number. hence, √5 is an irrational number. the square root of 5 is commonly also called "root 5". the root of a number "n" is represented as √n. Transcript. ex 1.2, 1 prove that √5 is irrational. we have to prove √5 is irrational let us assume the opposite, i.e., √5 is rational hence, √5 can be written in the form 𝑎 𝑏 where a and b (b≠ 0) are co prime (no common factor other than 1) hence, √𝟓 = 𝒂 𝒃 √5 b = a squaring both sides (√5b)2 = a2 5b2 = a2 𝒂^𝟐 𝟓 = b2 hence, 5 divides a2 so, 5 shall divide.

Irrational Numbers Definition And Application With Examples
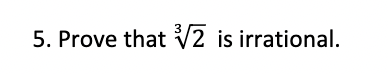
Solved 5 Prove That 32 Is Irrational Chegg

Comments are closed.