Prove Corollary 8 1 Using Theorem 8 1 And The Singular Value Decomposition

Solved Corollary 1 Corollary To Theorem 8 If Nimo An A Chegg Theorem. suppose ~a is obtained from a = u v > by truncating all but the k largest singular values i of a to zero. then, ~a minimizes both ka ~akfro and ka ~ak2 subject to the constraint that the column space of ~a has at most dimension k. The singular value decomposition (svd) more than just orthogonality,these basis vectors diagonalizethe matrix a: “a is diagonalized” av1 =σ1u1 av2 =σ2u2 avr =σrur (1) those singular valuesσ1 toσr will be positive numbers:σi is the length of avi. theσ’s go into a diagonalmatrix that is otherwise zero. that matrix isΣ.

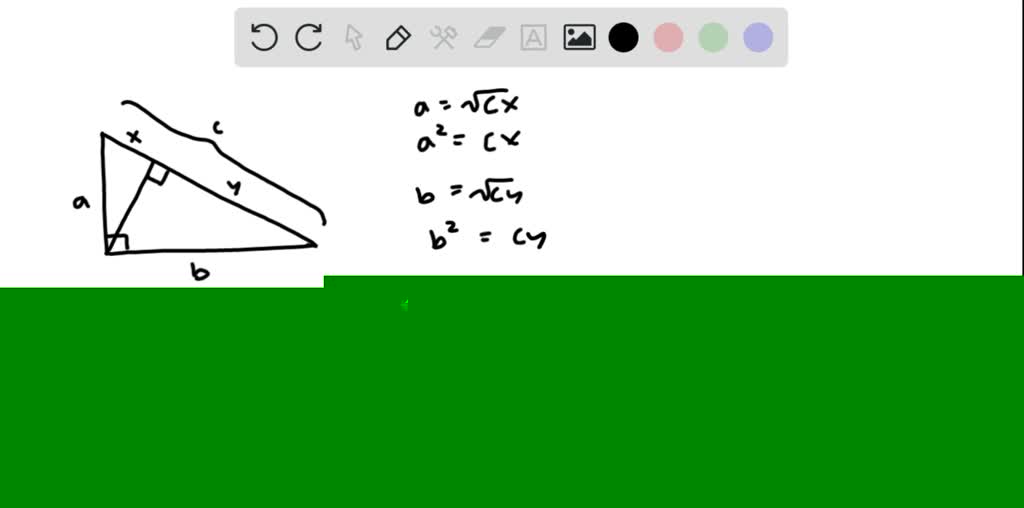
Solved Critical Thinking Use The Figure To Show How Corollary 8 1 3 Can Singular value decompositions. let a ∈ rm×n be a matrix. a singular triplet of a is a triplet (σ, u, v) such that. a0v = σu. σ is a singular value of a, u is a left singular vector and v is a right singular vector. a0au = σa0v = σ2u and aa0v = σau = σ2v. In a linear algebra and analysis course [it's a hybrid course between the two], we recently had the svd (singular value decomposition) theorem, and the prof. told us (due to lack of time without proof): corollary 2.39: let a = uΣvt be the singular value decomposition of a ∈ rm × n, where the singular values σ1 ≥ ⋯ ≥ σp ≥ 0, where. \[\begin{split} \sigma = \begin{bmatrix}\tilde{\sigma}\\ 0 \end{bmatrix} \end{split}\]. Find step by step linear algebra solutions and the answer to the textbook question prove corollary $8.1,$ using theorem $8.1$ and the singular value decomposition.

Visualization Of Theorem 1 It Follows Immediately From 8 Corollary 1 \[\begin{split} \sigma = \begin{bmatrix}\tilde{\sigma}\\ 0 \end{bmatrix} \end{split}\]. Find step by step linear algebra solutions and the answer to the textbook question prove corollary $8.1,$ using theorem $8.1$ and the singular value decomposition. A= pdpt: (1) a singular value decomposition (svd) is a generalization of this where ais an m nmatrix which does not have to be symmetric or even square. 1 singular values let abe an m nmatrix. before explaining what a singular value decom position is, we rst need to de ne the singular values of a. consider the matrix ata. this is a symmetric n. 1 construction the first singular value is defined as: σ 1 = sup ∥v∥=1 ∥av∥. remark 1. the first singular value is well defined, i.e., such av 1 ∈rn always exists. non rigorous argument: the function : v→∥av∥is continuous and with a compact domain. now one can findu 1 ∈rmwith ∥u 1∥= 1 such that av 1 = σ 1u 1.