Properties Of Real Numbers Andymath

Properties Of Real Numbers Andymath Andymath content has a unique approach to presenting mathematics. the clear explanations, strong visuals mixed with dry humor regularly get millions of views. we are open to collaborations of all types, please contact andy at tutoring@andymath for all enquiries. Properties of real numbers mathbitsnotebook (a1) a real number is a value that represents a quantity along a continuous number line. real numbers can be ordered. the symbol for the set of real numbers is , which is the letter r in the typeface "blackboard bold". the real numbers include: counting (natural) numbers () {1, 2, 3,.

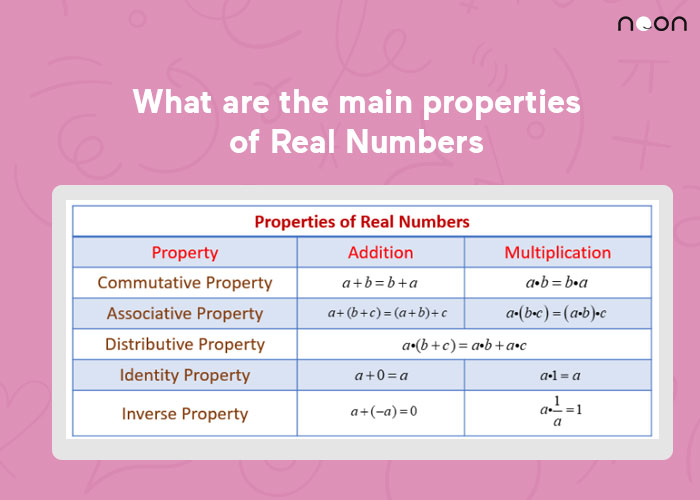
What Are The Main Properties Of Real Numbers A b is real 2 3 = 5 is real. a×b is real 6 × 2 = 12 is real . adding zero leaves the real number unchanged, likewise for multiplying by 1: identity example. a 0 = a 6 0 = 6. a × 1 = a 6 × 1 = 6 . for addition the inverse of a real number is its negative, and for multiplication the inverse is its reciprocal: additive inverse example. Commutative property. of addition if a and bare real numbers, then a b = b a. of multiplication if a and bare real numbers, then a · b = b · a. when adding or multiplying, changing the order gives the same result. the commutative property has to do with order. we subtract 9 − 8 and 8 − 9, and see that 9 − 8 ≠ 8 − 9. To keep it organized, i decided to divide the properties of real numbers into three (3) parts. the first one involves the addition operation. the second involves the operation of multiplication. while the third combines the operations of addition and multiplication. verbal description: if you add two real numbers, the sum is also a real number. A number and its reciprocal multiply to one. 1 a is the multiplicative inverse of a. properties of zero. for any real number a, a ⋅ 0 = 0 0 · a = 0 – the product of any real number and 0 is 0. 0 a = 0 for a ≠ 0 – zero divided by any real number except zero is zero. a 0 is undefined – division by zero is undefined.

Ppt 1 1 Properties Of Real Numbers Powerpoint Presentation Free To keep it organized, i decided to divide the properties of real numbers into three (3) parts. the first one involves the addition operation. the second involves the operation of multiplication. while the third combines the operations of addition and multiplication. verbal description: if you add two real numbers, the sum is also a real number. A number and its reciprocal multiply to one. 1 a is the multiplicative inverse of a. properties of zero. for any real number a, a ⋅ 0 = 0 0 · a = 0 – the product of any real number and 0 is 0. 0 a = 0 for a ≠ 0 – zero divided by any real number except zero is zero. a 0 is undefined – division by zero is undefined. The inverse properties: 1. if a is any real number, then there is a unique real number − a, such that. a (− a) = 0 and − a a = 0. the numbers a and − a are called additive inverses of each other. 2. if a is any nonzero real number, then there is a unique real number 1 a such that. a ⋅ 1 a = 1 and 1 a ⋅ a = 1. Scroll down the page for more examples and solutions using the properties of real numbers. properties of real numbers defines the properties of real numbers and then provides examples of the properties by rewriting and simplifying expressions.these include the distributive property, factoring, the inverse properties, the identity properties.

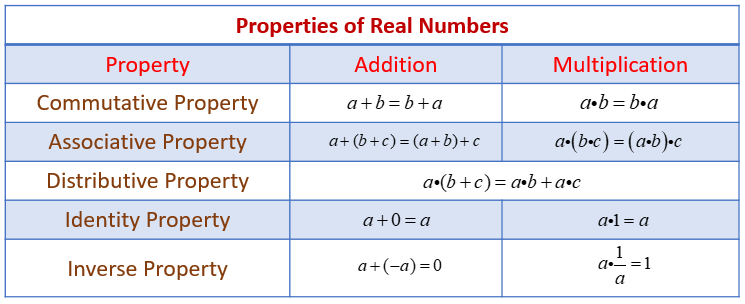
Properties Of Real Numbers Examples Solutions Worksheets Videos The inverse properties: 1. if a is any real number, then there is a unique real number − a, such that. a (− a) = 0 and − a a = 0. the numbers a and − a are called additive inverses of each other. 2. if a is any nonzero real number, then there is a unique real number 1 a such that. a ⋅ 1 a = 1 and 1 a ⋅ a = 1. Scroll down the page for more examples and solutions using the properties of real numbers. properties of real numbers defines the properties of real numbers and then provides examples of the properties by rewriting and simplifying expressions.these include the distributive property, factoring, the inverse properties, the identity properties.

Properties Of Real Numbers Andymath

Properties Of Real Numbers Teach Math Interactive