Proofs Of Pythagoras Theorem
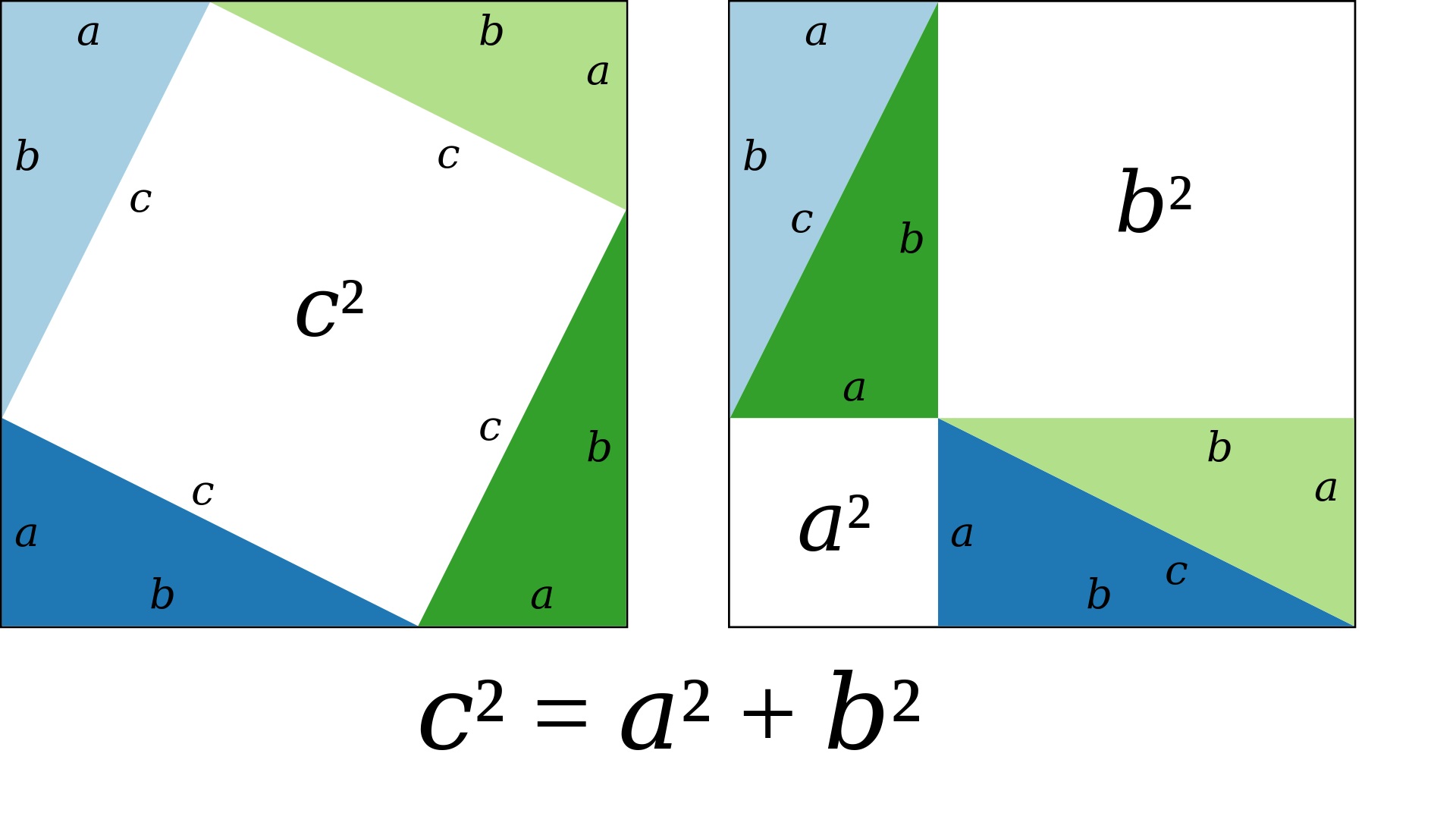
Pythagorean Theorem Proof Proof by rearrangement. pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see. The pythagorean theorem provides an equation to calculate the longer side of a right triangle by summing the squares of the other two sides. it is often phrased as. a2 b2 c2. in this equation, a.
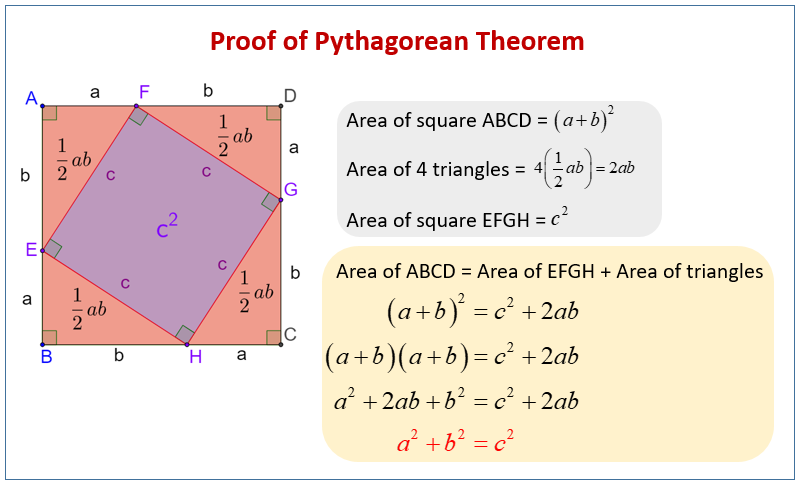
Proving The Pythagorean Theorem Math Liberty The hundreds of diagrams throughout [citation 1]—one for each proof—make it clear that its author e. loomis believed this was the only legitimate way to prove pythagoras’s theorem, which explains why he disqualified the many “trigonometric proofs” (called “cyclotopic” above), which would certainly have been known to someone who. In mathematics, the pythagorean theorem or pythagoras' theorem is a fundamental relation in euclidean geometry between the three sides of a right triangle. it states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. Pythagoras theorem (also called pythagorean theorem) is an important topic in mathematics, which explains the relation between the sides of a right angled triangle. the sides of the right triangle are also called pythagorean triples. the formula and proof of this theorem are explained here with examples.

How To Prove The Pythagorean Theorem 10 Steps With Pictures What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. Pythagoras theorem (also called pythagorean theorem) is an important topic in mathematics, which explains the relation between the sides of a right angled triangle. the sides of the right triangle are also called pythagorean triples. the formula and proof of this theorem are explained here with examples. Example 3: use the pythagoras theorem to find the hypotenuse of the triangle in which the sides are 8 units and 6 units respectively. solution: using the pythagoras theorem, hypotenuse 2 = base 2 height 2 = 8 2 6 2. this leads to hypotenuse 2 = 64 36 = 100. therefore, hypotenuse = √100 = 10 units. The pythagorean theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. so if a a and b b are the lengths of the legs, and c c is the length of the hypotenuse, then a^2 b^2=c^2 a2 b2 = c2.
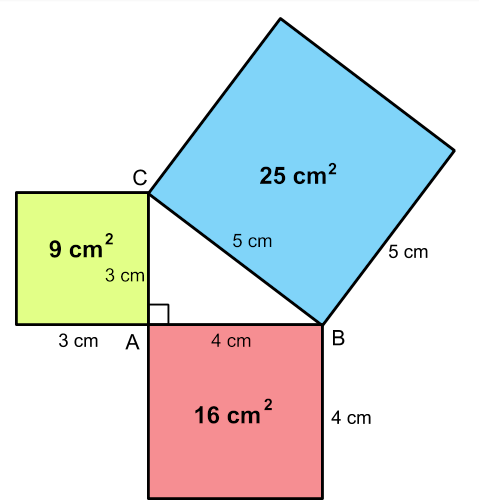
The Pythagorean Theorem Math Tutor Free Math For All Example 3: use the pythagoras theorem to find the hypotenuse of the triangle in which the sides are 8 units and 6 units respectively. solution: using the pythagoras theorem, hypotenuse 2 = base 2 height 2 = 8 2 6 2. this leads to hypotenuse 2 = 64 36 = 100. therefore, hypotenuse = √100 = 10 units. The pythagorean theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. so if a a and b b are the lengths of the legs, and c c is the length of the hypotenuse, then a^2 b^2=c^2 a2 b2 = c2.

How To Do Garfield S Proof Of The Pythagorean Theorem 10 Steps

Pythagorean Theorem Proof Lesson For Kids Study

Comments are closed.