Proof The Power Rule Of Derivatives For Natural Exponents Quick Math

Derivative Rules The Power Rule Chitown Tutoring Today we'll prove the power rule for derivatives, which will utilize the result of the last quick math video.follow me on instagram for previews, behind the. The power rule can be written as follows: f' (x^n) = nx^ {n 1} f ′(xn) = nxn−1. where. x x is the variable. n n is the value of the numerical exponent of variable x x. in polynomial functions, the power rule is also used by each term, and altogether supported by the sum difference of derivatives. in special cases of transcendental functions.
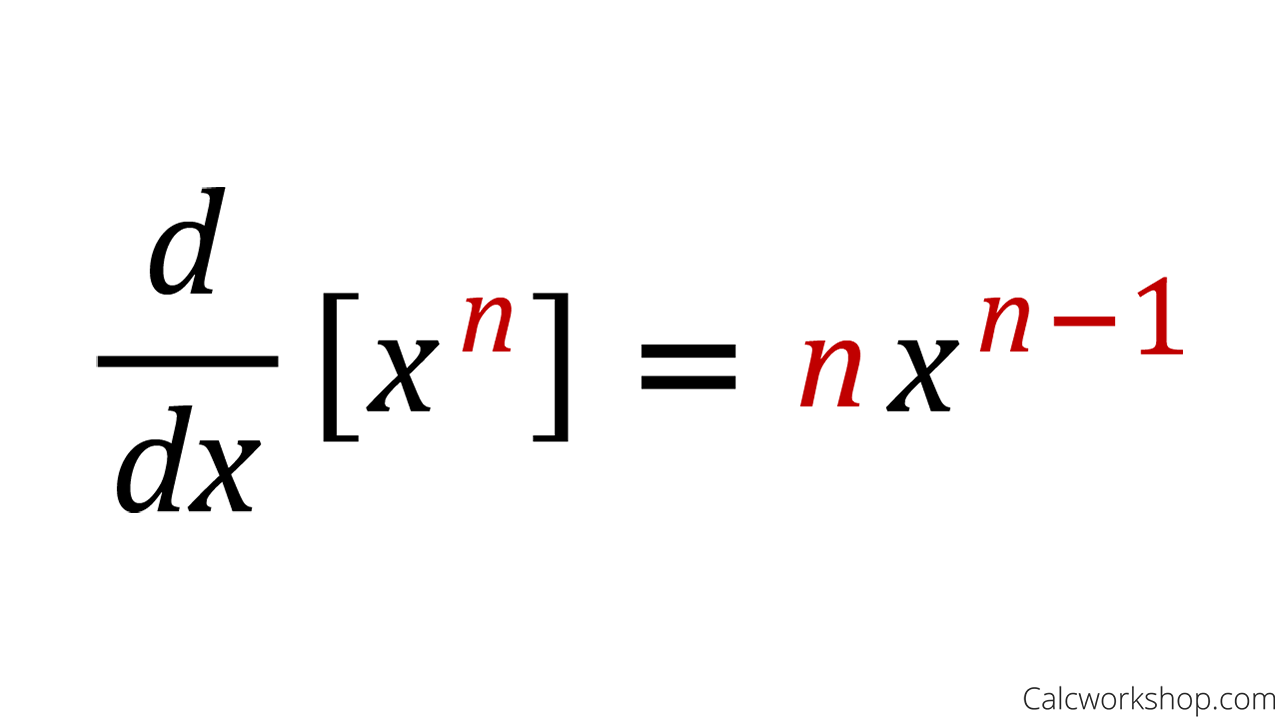
Power Rule How To W 9 Step By Step Examples The power rule tells us how to find the derivative of any expression in the form x n : d d x [x n] = n ⋅ x n − 1. the ap calculus course doesn't require knowing the proof of this rule, but we believe that as long as a proof is accessible, there's always something to learn from it. in general, it's always good to require some kind of proof. The power rule by repeatedly using product rule. though it is not a “proper proof,” it can still be good practice using mathematical induction. a common proof that is used is using the binomial theorem: the limit definition for x n would be as follows. using the binomial theorem, we get. subtract the x n. factor out an h. all of the terms. Power rule for exponents. the power rule for exponents is used when an exponent is raised to a power. for a positive integer x and integers m and n, we have the formula (x m) n = x mn. in this formula, we have two powers m and n which are multiplied by the simplification of the expression. let us consider some examples to understand it better:. Including the rules of exponents and the properties of various algebraic structures (integers, rational numbers, and real numbers). these constraints will prevent me from using. the derivative of a logarithm, the derivative of the exponential function, or the binomial theorem. most proofs i’ve seen use at least one of these. proof structure.

The Power Rule For Derivatives Youtube Power rule for exponents. the power rule for exponents is used when an exponent is raised to a power. for a positive integer x and integers m and n, we have the formula (x m) n = x mn. in this formula, we have two powers m and n which are multiplied by the simplification of the expression. let us consider some examples to understand it better:. Including the rules of exponents and the properties of various algebraic structures (integers, rational numbers, and real numbers). these constraints will prevent me from using. the derivative of a logarithm, the derivative of the exponential function, or the binomial theorem. most proofs i’ve seen use at least one of these. proof structure. The 8 didn’t have a negative exponent, so it stayed. derivatives of functions with radicals (square roots and other roots) another useful property from algebra is the following. using this rule, we can take a function written with a root and find its derivative using the power rule. example. find the derivative of the function. Applications of power rule. the power rule states that the derivative of x to the power n is equal to n times x to the power n 1. in other words, if we have a polynomial function [tex]f(x) = a n x^n a {n 1} x^{n 1} … a 1 x a 0, [ tex] we can differentiate it by taking the derivative of each term using the power rule and adding the results.

Proof Of The Power Rule Youtube The 8 didn’t have a negative exponent, so it stayed. derivatives of functions with radicals (square roots and other roots) another useful property from algebra is the following. using this rule, we can take a function written with a root and find its derivative using the power rule. example. find the derivative of the function. Applications of power rule. the power rule states that the derivative of x to the power n is equal to n times x to the power n 1. in other words, if we have a polynomial function [tex]f(x) = a n x^n a {n 1} x^{n 1} … a 1 x a 0, [ tex] we can differentiate it by taking the derivative of each term using the power rule and adding the results.

Comments are closed.