Problems On Common Tangents To Two Circles Transverse Common Tangent
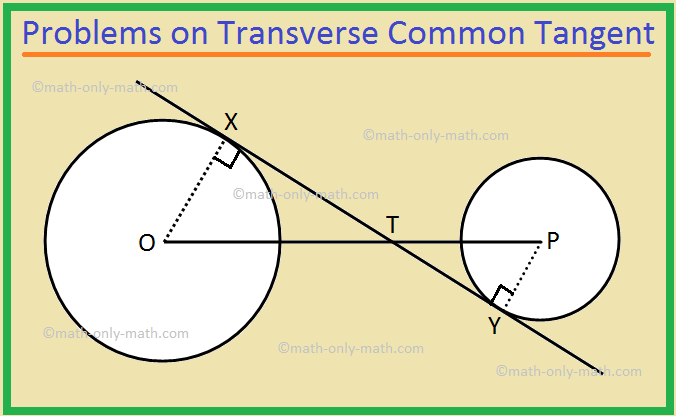
Problems On Common Tangents To Two Circles Transverse Common Tangent Therefore, bc = 8√2 cm. 2. prove that a transverse common tangent drawn to two circles divides the line joining their centres into the ratio of their radii. solution: given: two circles with centres o and p, and radii ox and py respectively. the transverse common tangent xy touches them at x and y respectively. xy cuts op at t. (ii) when circle are apart from each other then \(c 1\)\(c 2\) > \(r 1\) \(r 2\) and in this case there will be four common tangents. direct and transverse common tangents. let two circles having centers c1 and c2 and radii, r1 and r2 and c1c2 is the distance between their centres. lines pq and rs are called transverse or indirect or internal.
Problems On Common Tangents To Two Circles Transverse Common Tangent A common tangent is called transverse if the two circles lie on opposite sides of it. in the following situation, we have two circles lying externally to each other, and exactly two transverse common tangents: for two circles touching each other externally, there will be exactly one transverse common tangent (and of course, two direct common. 7. find the equations of the common tangents to the 2 circles: (x − 2)2 y2 = 9 and. (x − 5)2 (y − 4)2 = 4. i've tried to set the equation to be y = ax b, substitute this into the 2 equations and set the discriminant to zero, we then get a simultaneous quadratic equations. but they are really difficult to solve. Here’s how to solve it: draw the segment connecting the centers of the two circles and draw the two radii to the points of tangency (if these segments haven’t already been drawn for you). the following figure shows this step. note that the given distance of 8 between the circles is the distance between the outsides of the circles along the. If two circles touch each other externally at one point, they will have three common tangents. 5. four common tangents: if two circles do not touch or intersect each other and one does not lie inside the other, they will have four common tangents. ab and cd are called direct common tangents, and mn and xy are called transverse common tangents.

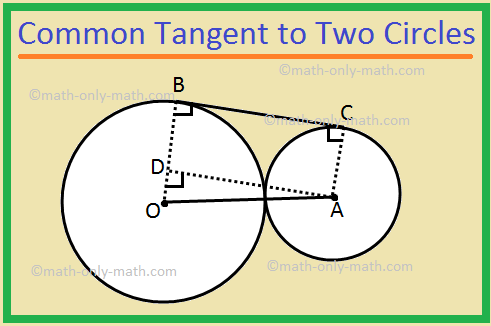
Solving Circle Geometry Tangent Transverse Tangent Common To Two Here’s how to solve it: draw the segment connecting the centers of the two circles and draw the two radii to the points of tangency (if these segments haven’t already been drawn for you). the following figure shows this step. note that the given distance of 8 between the circles is the distance between the outsides of the circles along the. If two circles touch each other externally at one point, they will have three common tangents. 5. four common tangents: if two circles do not touch or intersect each other and one does not lie inside the other, they will have four common tangents. ab and cd are called direct common tangents, and mn and xy are called transverse common tangents. We will discuss about the important properties of transverse common tangents. i. the two transverse common tangents drawn to two circles are equal in length. given: wx and yz are two transverse common tangents drawn to the two given circles with centres o and p. wx and yz. Circles intersecting at two points. same here. we’ll use the method in the first case for the direct common tangents. circles touching each other internally. the tangent here is perpendicular to the line joining the centres, and passes through the point which divides c 1 c 2 in the ratio r 1: r 2 externally.

Common Tangents To Two Circles Geometry Youtube We will discuss about the important properties of transverse common tangents. i. the two transverse common tangents drawn to two circles are equal in length. given: wx and yz are two transverse common tangents drawn to the two given circles with centres o and p. wx and yz. Circles intersecting at two points. same here. we’ll use the method in the first case for the direct common tangents. circles touching each other internally. the tangent here is perpendicular to the line joining the centres, and passes through the point which divides c 1 c 2 in the ratio r 1: r 2 externally.
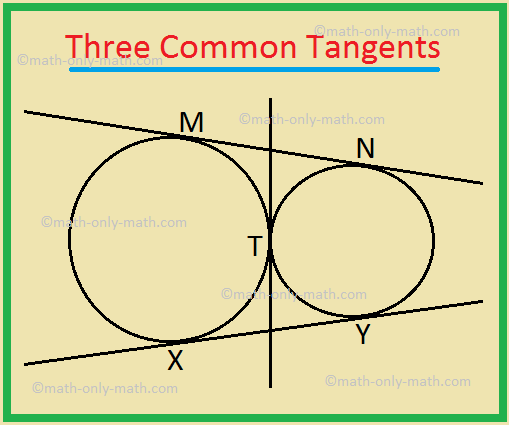
Common Tangents To Two Circles Transverse Common Tangents

Comments are closed.