Problem Solving Involving Percent
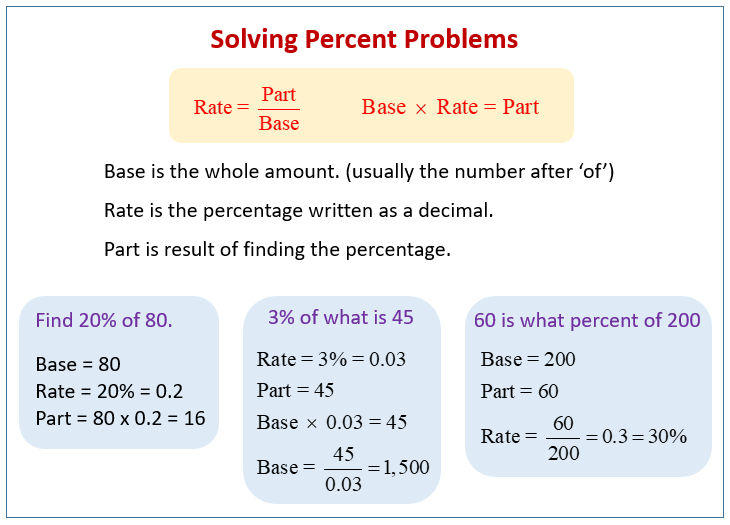
Solving Percent Problems Examples Solutions Worksheets Videos Problems involving percents have any three quantities to work with: the percent, the amount, and the base. the percent has the percent symbol (%) or the word “percent.” in the problem above, 15% is the percent off the purchase price. the base is the whole amount. in the problem above, the whole price of the guitar is $220, which is the base. Now we can solve our equation for x. 10 = 80x original equation. 10 80 = 80x 80 divide both sides by 80. 1 8 = x reduce: 10 80 = 1 8. 0.125 = x divide: 1 8 = 0.125. but we must express our answer as a percent. to do this, move the decimal two places to the right and append a percent symbol.

Problem Solving With Percents Practice Amped Up Learning Now we will apply the concept of percentage to solve various real life examples on percentage. solved examples on percentage: 1. in an election, candidate a got 75% of the total valid votes. if 15% of the total votes were declared invalid and the total numbers of votes is 560000, find the number of valid vote polled in favour of candidate. Thus, this is the type 3 percentage problem. apply the formula (***) to calculate the georgetown population at the end 2009. you have. . in other words, 1500 3 = 500 was the measure of 1% of population, or 1 100 part. then 100%, the whole population, was 100 times more, or 500 x 100 = 50000. Subtract the two numbers to find the amount of decrease. using this result as the amount and the original number as the base, find the unknown percent. again, we always use the original number for the base, the number that occurred earlier in time. for a percent decrease, this is the larger of the two numbers. exercises 4.2.1. Percent problems percent problems – example 1: \(2.5\) is what percent of \(20\)? solution: in this problem, we are looking for the percent. use the following equation: \(\color{blue}{percent} = \color{ black }{part} \ ÷\) base \(→\) percent \(=2.5 \ ÷ \ 20=0.125=12.5\%\) the absolute best books to ace pre algebra to algebra ii.

Solving Percent Problems Worksheet Db Excel Subtract the two numbers to find the amount of decrease. using this result as the amount and the original number as the base, find the unknown percent. again, we always use the original number for the base, the number that occurred earlier in time. for a percent decrease, this is the larger of the two numbers. exercises 4.2.1. Percent problems percent problems – example 1: \(2.5\) is what percent of \(20\)? solution: in this problem, we are looking for the percent. use the following equation: \(\color{blue}{percent} = \color{ black }{part} \ ÷\) base \(→\) percent \(=2.5 \ ÷ \ 20=0.125=12.5\%\) the absolute best books to ace pre algebra to algebra ii. Percent proportion. problems involving the percent equation can also be solved with the proportion: percent amount (is) =. 100 base (of) when the percent is given, drop the percent sign and place the percent over 100. cross multiply to solve the proportion. example 2: 27 is 45% of what number?. Find a percent of a quantity as a rate per 100 (for example, 30\% of a quantity means \frac{30}{100} times the quantity); solve problems involving finding the whole, given a part and the percent. how to find the percent.

Basic Percentage Word Problems Percent proportion. problems involving the percent equation can also be solved with the proportion: percent amount (is) =. 100 base (of) when the percent is given, drop the percent sign and place the percent over 100. cross multiply to solve the proportion. example 2: 27 is 45% of what number?. Find a percent of a quantity as a rate per 100 (for example, 30\% of a quantity means \frac{30}{100} times the quantity); solve problems involving finding the whole, given a part and the percent. how to find the percent.

Comments are closed.