Ppc 4 5 Graphs Of Sine And Cosine Functions Part 2 Math
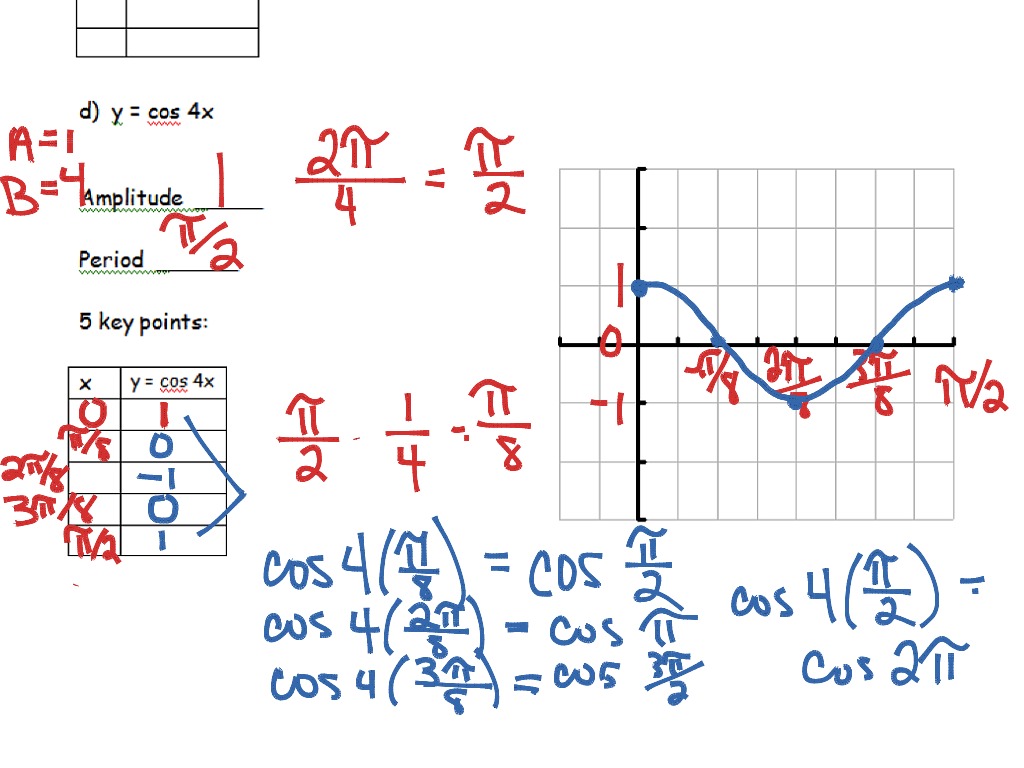
Ppc 4 5 Graphs Of Sine And Cosine Functions Part 2 Math Graphing sine and cosine functions. any equation of the form y = a sin b ( x − c ) d with a ≠ 0 and b ≠ 0 is a sine function. its graph is. called a sine wave, sinusoidal wave, or sinusoid. the graph of any sine function is a transformation of the graph of y = sin x . assume x is in radians unless the problem specifically states that it. The smallest such value is the period. the basic sine and cosine functions have a period of \(2\pi\). the function \(\sin x\) is odd, so its graph is symmetric about the origin. the function \(\cos x\) is even, so its graph is symmetric about the y axis. the graph of a sinusoidal function has the same general shape as a sine or cosine function.
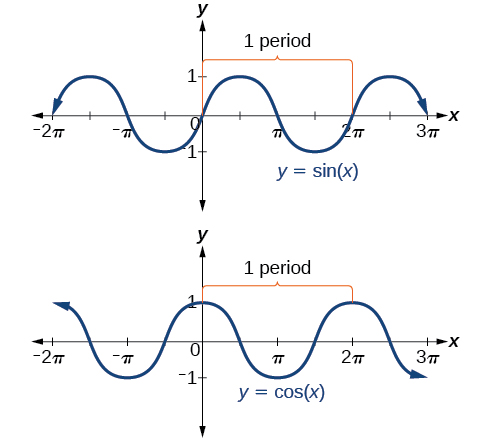
Section 4 5 Graphs Of The Sine And Cosine Function Precalculus In this section, you will study techniques for sketching the graphs of the sine and cosine functions. the graph of the sine function is a sine curve. in figure 4.47, the black portion of the graph represents one period of the function and is called one cycle of the sine curve. the gray portion of the graph indicates that the basic sine curve. Appc 3.4 ca2.pdf. file size: 261 kb. file type: pdf. download file. ap learning objectives: 3.4.a construct representations of the sine and cosine functions using the unit circle. *ap® is a trademark registered and owned by the collegeboard, which was not involved in the production of, and does not endorse, this site. The sine and cosine functions have several distinct characteristics: they are periodic functions with a period of 2π. the domain of each function is (− ∞, ∞) (− ∞, ∞) and the range is [− 1, 1] [− 1, 1] . the graph of y = sinx y = sin x. is symmetric about the origin, because it is an odd function. Y=a\sin (bx−c) d. y=a\cos (bx−c) d. the graph could represent either a sine or a cosine function that is shifted and or reflected. when x=0, the graph has an extreme point, (0,0). since the cosine function has an extreme point for x=0, let us write our equation in terms of a cosine function.
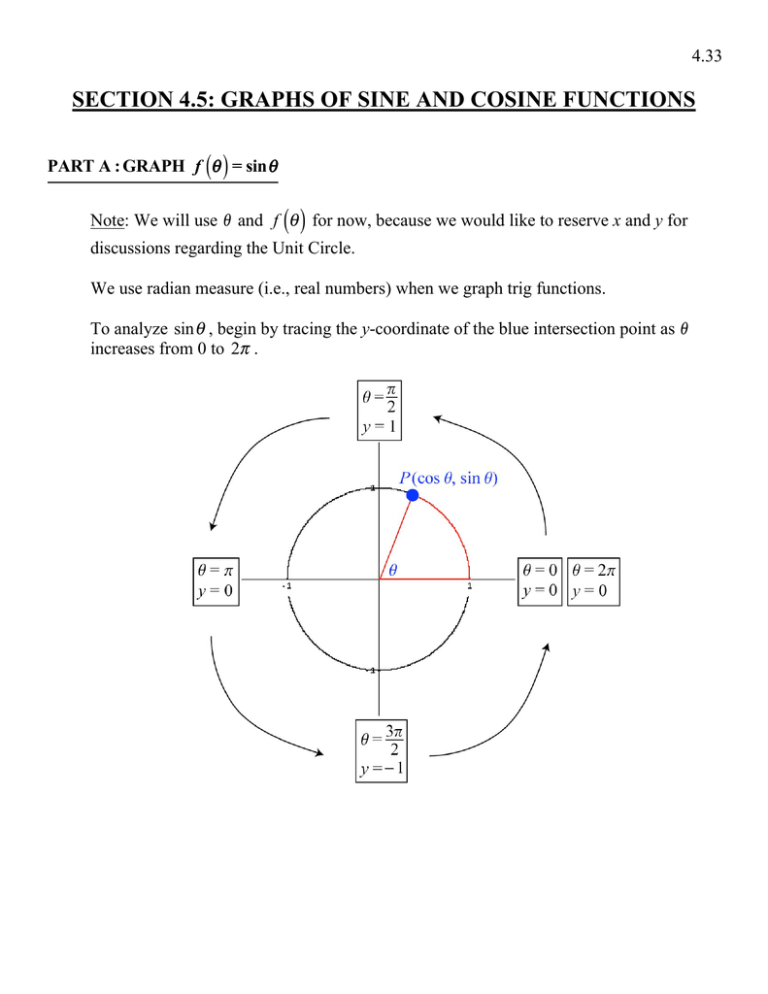
Section 4 5 Graphs Of Sine And Cosine Functions The sine and cosine functions have several distinct characteristics: they are periodic functions with a period of 2π. the domain of each function is (− ∞, ∞) (− ∞, ∞) and the range is [− 1, 1] [− 1, 1] . the graph of y = sinx y = sin x. is symmetric about the origin, because it is an odd function. Y=a\sin (bx−c) d. y=a\cos (bx−c) d. the graph could represent either a sine or a cosine function that is shifted and or reflected. when x=0, the graph has an extreme point, (0,0). since the cosine function has an extreme point for x=0, let us write our equation in terms of a cosine function. 2.sketch the graph of y= 1 2 cosx. the amplitude of the function is 1 2. the negative sign will \ ip" the graph upside down. 6 (the hash marks on the x axis are in increments of ˇ=2.) now, we will focus on functions of the form y= asin(bx) and y= acos(bx). we will assume that b>0 (if bis negative, we can use that sine is an odd function and. Investigating sinusoidal functions. as we can see, sine and cosine functions have a regular period and range. if we watch ocean waves or ripples on a pond, we will see that they resemble the sine or cosine functions. however, they are not necessarily identical. some are taller or longer than others.
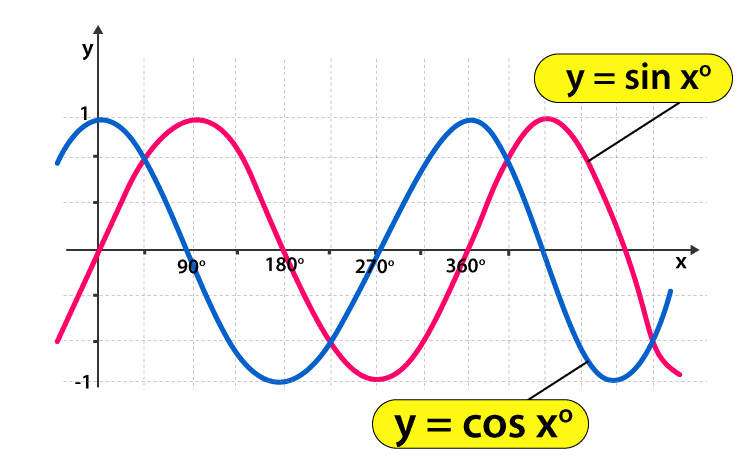
Trigonometry Graphs For Sine Cosine And Tangent Functions 2.sketch the graph of y= 1 2 cosx. the amplitude of the function is 1 2. the negative sign will \ ip" the graph upside down. 6 (the hash marks on the x axis are in increments of ˇ=2.) now, we will focus on functions of the form y= asin(bx) and y= acos(bx). we will assume that b>0 (if bis negative, we can use that sine is an odd function and. Investigating sinusoidal functions. as we can see, sine and cosine functions have a regular period and range. if we watch ocean waves or ripples on a pond, we will see that they resemble the sine or cosine functions. however, they are not necessarily identical. some are taller or longer than others.

Comments are closed.