Piecewise Function Questions And Answers
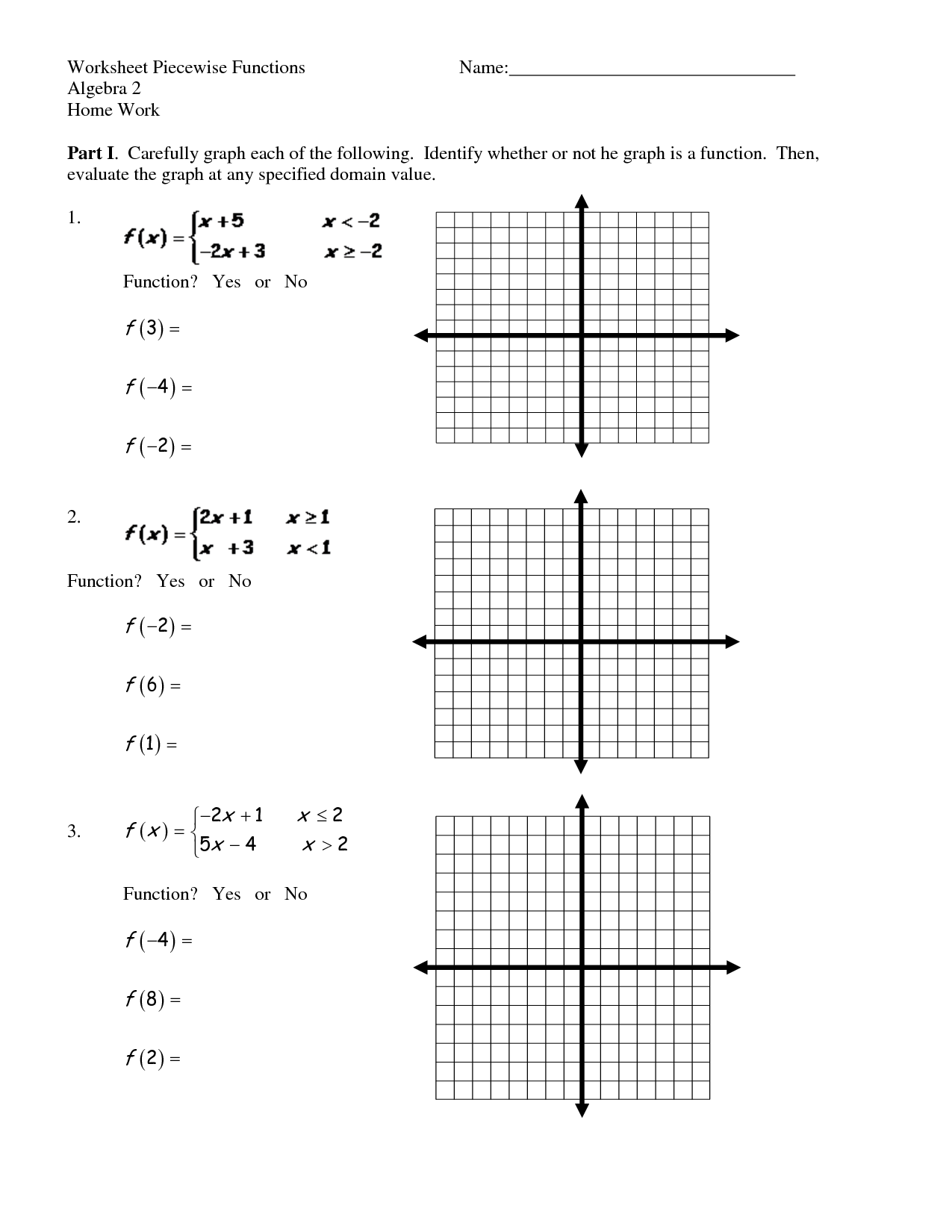
Worksheets Piecewise Functions Answer Key G: simplify combination functions and find their domains. exercise 2.4e. ★ for each pair of functions f and g given below, find and simplify the combination functions f g, f − g, fg, and f g. state the domain of each combination functions in interval notation. 71. f(x) = x2 2x, g(x) = 6 − x2. Write a piecewise function to represent individual cost of a t shirt as function of . the number of shirts made. graph it! label the graph! 7. sat prep below are sample sat questions. the sat is the main standardized test that colleges look at for admission. one is multiple choices; the other is free response where you must grid in your answer.

Piecewise Functions Word Problems Worksheet With Answers Pdf Function A function can be in pieces. we can create functions that behave differently based on the input (x) value. a function made up of 3 pieces. example: imagine a function. when x is less than 2, it gives x2, when x is exactly 2 it gives 6. when x is more than 2 and less than or equal to 6 it gives the line 10−x. it looks like this:. The following math revision questions are provided in support of the math tutorial on piecewise functions. in addition to this tutorial, we also provide revision notes, a video tutorial, revision questions on this page (which allow you to check your understanding of the topic and calculators which provide full, step by step calculations for each of the formula in the piecewise functions tutorials. Piecewise function. at least 2 equations, each of which applies to a different part of the function's domain. ∞. infinity. <. less than. graphing piecewise functions given the function, and writing the functions given the graph! learn with flashcards, games, and more — for free. Graphing piecewise functions both of the following notations can be used to describe a piecewise function over the function’s domain: f(x) = ¯ ® 5 2x [2,6] [ 5,2) if if or f(x) = ,2 6, 5 2 d d d x x 3. complete the following table of values for the piecewise function over the given domain. x f(x) 5 3 0 1 1.7 1.9 2 2.2 4 6 4.
Solved Piecewise Answer The Following Piecewise Functions Example Piecewise function. at least 2 equations, each of which applies to a different part of the function's domain. ∞. infinity. <. less than. graphing piecewise functions given the function, and writing the functions given the graph! learn with flashcards, games, and more — for free. Graphing piecewise functions both of the following notations can be used to describe a piecewise function over the function’s domain: f(x) = ¯ ® 5 2x [2,6] [ 5,2) if if or f(x) = ,2 6, 5 2 d d d x x 3. complete the following table of values for the piecewise function over the given domain. x f(x) 5 3 0 1 1.7 1.9 2 2.2 4 6 4. Piecewise functions. select an answer from the options below and click submit. question 1. r (x)=. 39,0≤x<15. 0.04x2−3.6x 84,15 ≤x<65. 1 2 x− 27 2,x≥65. r of x is equal to 39 for x greater than or equal to 0 and less than 15, r of x is equal to four hundredths x squared minus three and six tenths x plus 84 for x greater than or equal. Piecewise function examples. example 1: graph the piecewise function f (x) = {−2x, −1≤ x <0 x2, 0 ≤ x <2 f (x) = {− 2 x, − 1 ≤ x <0 x 2, 0 ≤ x <2. solution: let us make tables for each of the given intervals using their respective definitions of the function. let us just plot them and join them by curves.
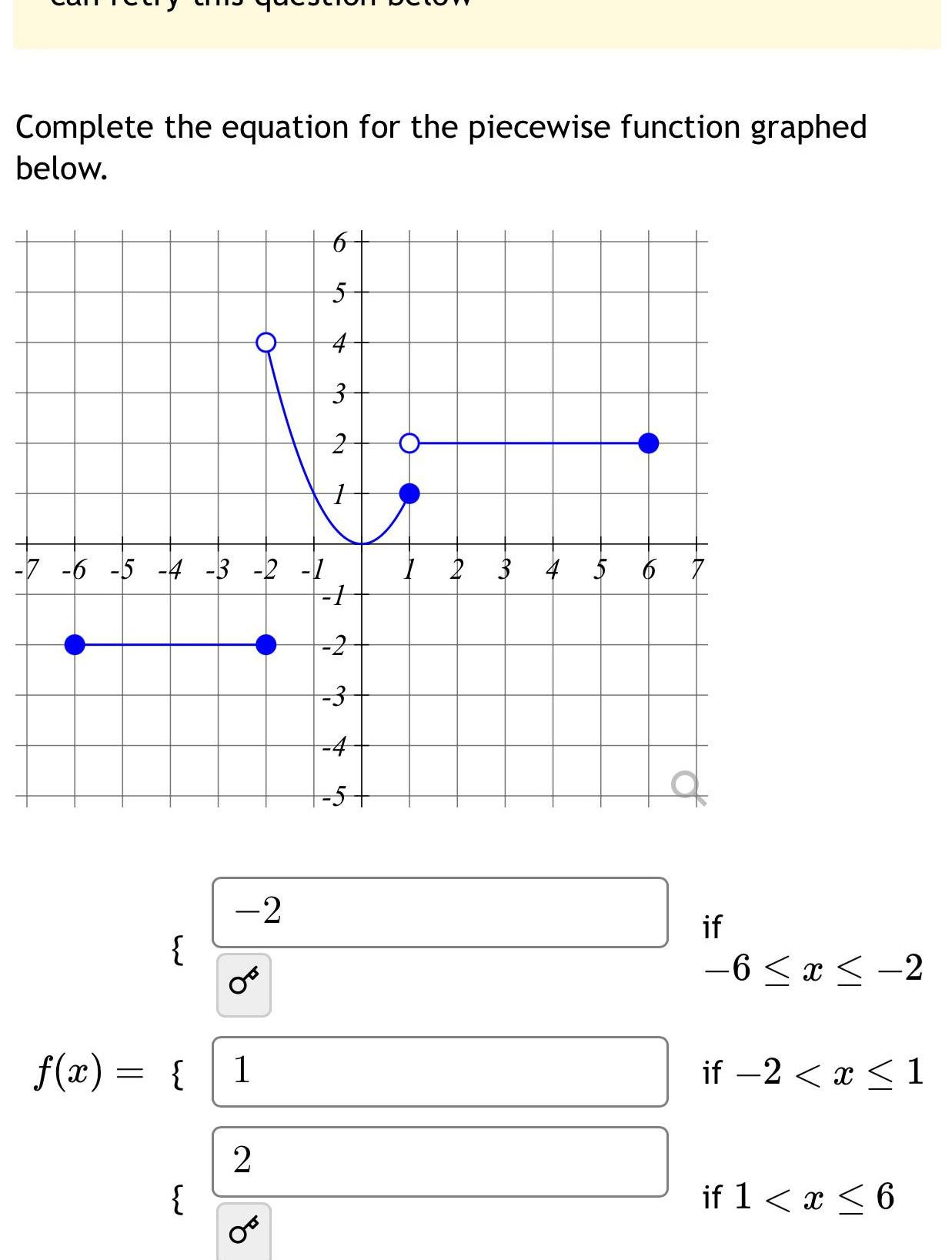
Answered Complete The Equation For The Piecewise Function Gr Piecewise functions. select an answer from the options below and click submit. question 1. r (x)=. 39,0≤x<15. 0.04x2−3.6x 84,15 ≤x<65. 1 2 x− 27 2,x≥65. r of x is equal to 39 for x greater than or equal to 0 and less than 15, r of x is equal to four hundredths x squared minus three and six tenths x plus 84 for x greater than or equal. Piecewise function examples. example 1: graph the piecewise function f (x) = {−2x, −1≤ x <0 x2, 0 ≤ x <2 f (x) = {− 2 x, − 1 ≤ x <0 x 2, 0 ≤ x <2. solution: let us make tables for each of the given intervals using their respective definitions of the function. let us just plot them and join them by curves.

Comments are closed.