Parallel Lines And Proportional Parts Triangle Proportionality
Triangle Proportionality Theorem With Proof And Examples Owlcation Utilize the given values af = 4 and fd = 6, and create a proportionality equation. ae ec = af fd. ae ec = 4 6. create the proportionality formula for the more big triangle abc. since the value of ae ec obtained from the previous equation is 4 6, substitute this value to the proportionality equation shown below. To prove the triangle proportionality theorem, consider a triangle abc with a line de parallel to bc (image below) as parallel lines form congruent angles, then: ∠ade ≅ ∠abc and ∠aed ≅ ∠acb. from the aa similarity criteria: abc ~ ade. as the triangles are proportional: ab ad = ac ae. using the denominator subtraction property:.

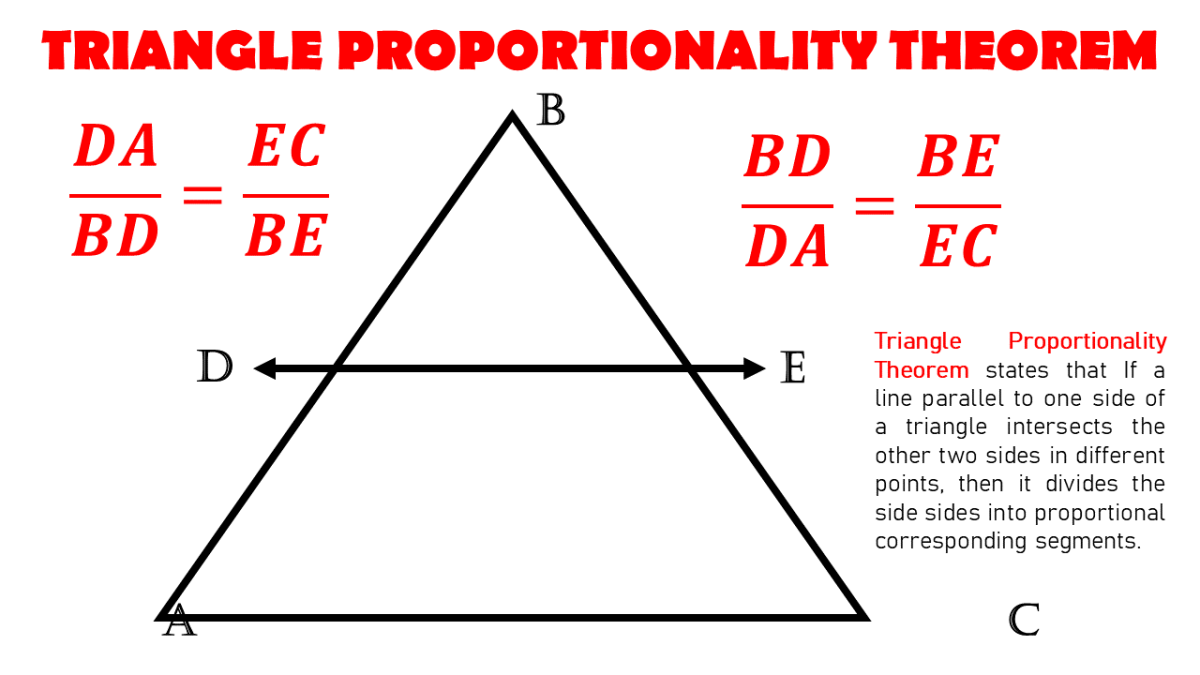
Solving Proportional Parts In Triangles And Parallel Lines Geometry Triangle proportionality theorem. the triangle proportionality theorem states that if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. we can extend this theorem to a situation outside of triangles where we have multiple parallel lines cut by transversals. According to the triangle proportionality theorem, the ratio of ps to sq is equal to the ratio of pt to tr. p s s q = p t t r. 8 12 = p t t r. ⇒ 2 3 = p t t r. ⇒ p t: t r = 2: 3. check whether the line pq is parallel to the bc or not. solution: a p = 6, b p = 9, a q = 5, and c q = 7.5. a p b p = 6 9 = 2 3. Parallel lines and proportionality. in the triangle proportionality theorem , we have seen that parallel lines cut the sides of a triangle into proportional parts. similarly, three or more parallel lines also separate transversals into proportional parts. if three or more parallel lines intersect two transversals, then they cut off the. The triangle proportionality theorem is a theorem that states that if we draw a line parallel to one side of a triangle so that it intersects the remaining two sides, then both sides are divided equally. if a line is drawn parallel to one side of a triangle, it is called the mid segment of the triangle.
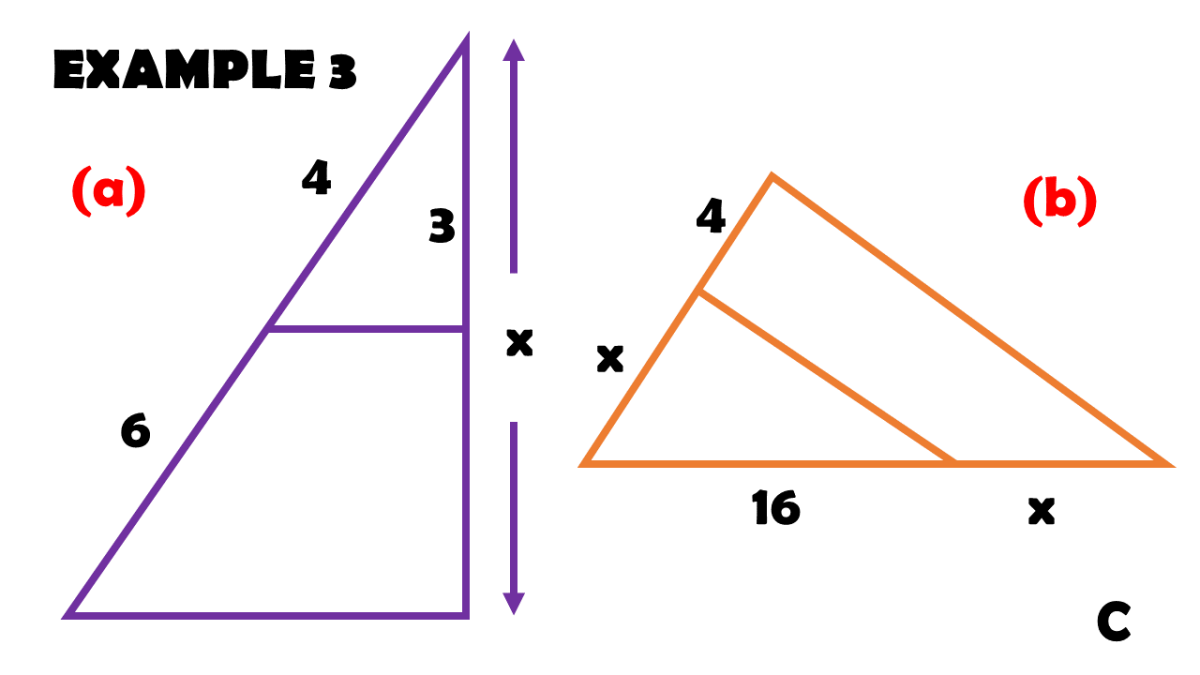
Triangle Proportionality Theorem With Proof And Examples Owlcation Parallel lines and proportionality. in the triangle proportionality theorem , we have seen that parallel lines cut the sides of a triangle into proportional parts. similarly, three or more parallel lines also separate transversals into proportional parts. if three or more parallel lines intersect two transversals, then they cut off the. The triangle proportionality theorem is a theorem that states that if we draw a line parallel to one side of a triangle so that it intersects the remaining two sides, then both sides are divided equally. if a line is drawn parallel to one side of a triangle, it is called the mid segment of the triangle. Construction: join the vertex b of Δabc to q and the vertex c to p to form the lines bq and cp. draw qn⊥ ab and pm⊥ac as shown in the given figure. proof: hence, the triangle proportionality theorem is proved. also, ∆abc and ∆apq satisfy the required conditions for similar triangles as stated above. therefore, it can be concluded that. A midsegment connects the midpoints of two sides of a triangle or the non parallel sides of a trapezoid. parallel: two or more lines are parallel when they lie in the same plane and never intersect. these lines will always have the same slope. proportion: a proportion is an equation that shows two equivalent ratios. triangle proportionality theorem.

Comments are closed.