Optimization Problems Minimum Cost Garden

Optimization Problems Minimum Cost Garden Youtube Walkthrough of a solution to a calculus optimization problem where we find the dimensions of a garden that minimizes the cost of construction, given some inf. The basic idea of the optimization problems that follow is the same. we have a particular quantity that we are interested in maximizing or minimizing. however, we also have some auxiliary condition that needs to be satisfied. for example, in example 4.32, we are interested in maximizing the area of a rectangular garden. certainly, if we keep.
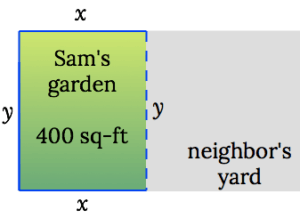
Garden Fence Optimization Problem Matheno Matheno The steps: 1. draw a picture of the physical situation. see the figure. we’ve called the width of the garden x (the top and bottom portions of the fence), and the length of the garden y (the left and right sides). note also that the total area of sam’s garden must be . 2. Step 4: from figure 4.7.5, the line segment of y miles forms the hypotenuse of a right triangle with legs of length 2 mi and 6 − x mi. therefore, by the pythagorean theorem, 22 (6 − x)2 = y2, and we obtain y = √(6 − x)2 4. thus, the total time spent traveling is given by the function. t(x) = x 8 √(6 − x)2 4 3. 1 1. find two positive integers such that their sum is 10, 10, and minimize and maximize the sum of their squares. for the following exercises, consider the construction of a pen to enclose an area. you have 400\phantom {\rule {0.2em} {0ex}}\text {ft} 400ft of fencing to construct a rectangular pen for cattle. Step 1: draw a rectangular box and introduce the variable to represent the length of each side of the square base; let represent the height of the box. let denote the surface area of the open top box. figure 8. we want to minimize the surface area of a square based box with a given volume.

Ppt Optimization Problems Powerpoint Presentation Free Download Id 1 1. find two positive integers such that their sum is 10, 10, and minimize and maximize the sum of their squares. for the following exercises, consider the construction of a pen to enclose an area. you have 400\phantom {\rule {0.2em} {0ex}}\text {ft} 400ft of fencing to construct a rectangular pen for cattle. Step 1: draw a rectangular box and introduce the variable to represent the length of each side of the square base; let represent the height of the box. let denote the surface area of the open top box. figure 8. we want to minimize the surface area of a square based box with a given volume. Introduction to optimization using calculus 1 setting up and solving optimization problems with calculus consider the following problem: a landscape architect plans to enclose a 3000 square foot rectangular region in a botan ical garden. she will use shrubs costing $25 per foot along three sides and fencing costing $10 per foot along the fourth. 4.7 optimization problems p. 5 9 example 2. cost minimization a rectangular garden of area 8,400 square feet is to be fenced off and then divided into 3 regions by 2 parallel fences across the interior of the garden. the fencing for the outside costs $9 per running foot, while that the interior dividing fence costs $12 per running foot.

Optimization Calculus Maximizing Area Of Garden Worked Example 7 Introduction to optimization using calculus 1 setting up and solving optimization problems with calculus consider the following problem: a landscape architect plans to enclose a 3000 square foot rectangular region in a botan ical garden. she will use shrubs costing $25 per foot along three sides and fencing costing $10 per foot along the fourth. 4.7 optimization problems p. 5 9 example 2. cost minimization a rectangular garden of area 8,400 square feet is to be fenced off and then divided into 3 regions by 2 parallel fences across the interior of the garden. the fencing for the outside costs $9 per running foot, while that the interior dividing fence costs $12 per running foot.

Optimization Calculus Minimizing Cost Youtube
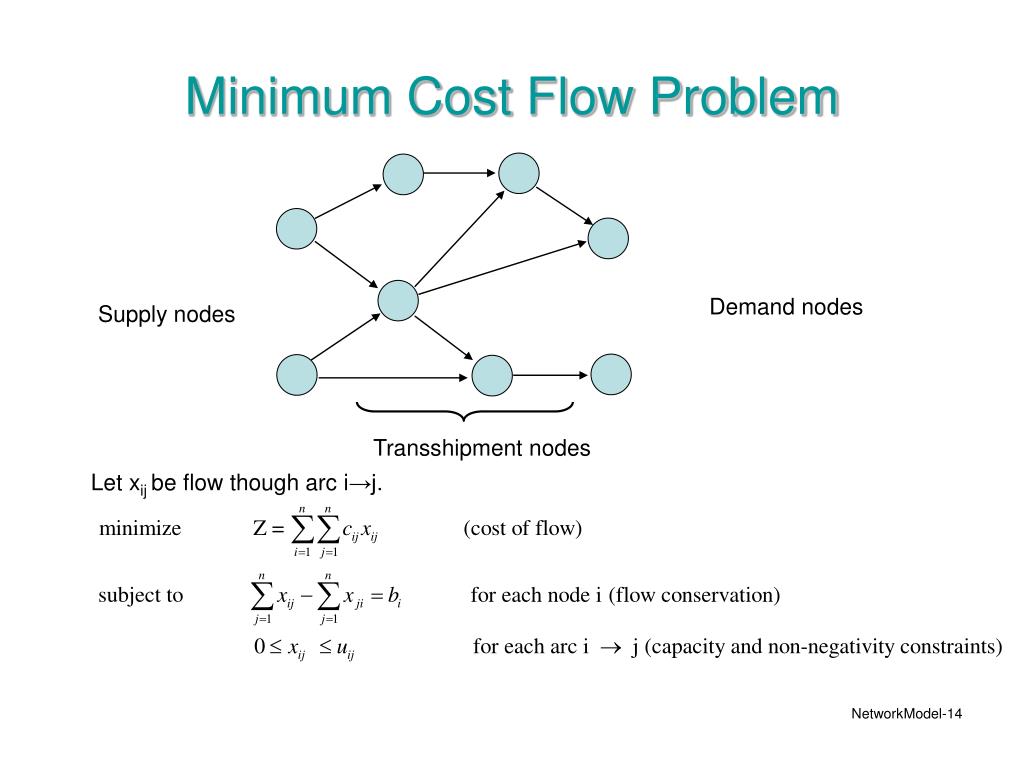
Ppt Network Optimization Models Powerpoint Presentation Free

Comments are closed.