Number Systems Decimal Binary And Hexadecimal 1 Basen
Number Systems Decimal Binary And Hexadecimal 1 Basen Hex numeral system. numeral system conversion table. numeral system. b numeral system base. dn the n th digit. n can start from negative number if the number has a fraction part. n 1 the number of digits. binary numeral system base 2. binary numbers uses only 0 and 1 digits. Count up until just before the "base number", then start at 0 again, but first you add 1 to the number on your left. binary numbers. binary numbers are just "base 2" instead of "base 10". so you start counting at 0, then 1, then you run out of digits so you start back at 0 again, but increase the number on the left by 1. like this:.

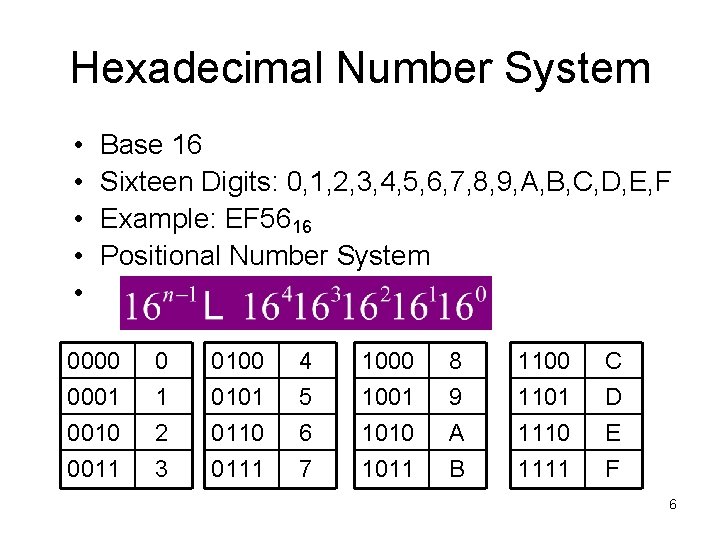
Number Systems Decimal Binary And Hexadecimal 1 Basen Based on the base value and the number of allowed digits, number systems are of many types. the four common types of number systems are: decimal number system; binary number system; octal number system; hexadecimal number system; decimal number system. a number system with a base value of 10 is termed a decimal number system. it uses 10 digits. Thus, it has fewer digits than the decimal number system. along with the binary numbers system, octal number systems are used in computers. 7 8, 47 8, and 1681 8 are examples of octal numbers. hexadecimal number system (base 16) the hexadecimal number system uses sixteen digits and alphabets. it includes numbers 0 to 9, as in the decimal number. Converting them to hexadecimal will give us 9, e, and 6. so our number will be 9e6 in hexadecimal. converting hexadecimal to binary. now we will change the hexadecimal number a1d 16 to binary. we begin by converting each separate digit to its decimal counterpart. a, 1, and d therefore become 10, 1, and 13 respectively. Number systems and bases. base systems like binary and hexadecimal seem a bit strange at first. the key is understanding how different systems “tick over” like an odometer when they are full. base 10, our decimal system, “ticks over” when it gets 10 items, creating a new digit. we wait 60 seconds before “ticking over” to a new minute.

Number Systems Decimal Binary And Hexadecimal 1 Basen Converting them to hexadecimal will give us 9, e, and 6. so our number will be 9e6 in hexadecimal. converting hexadecimal to binary. now we will change the hexadecimal number a1d 16 to binary. we begin by converting each separate digit to its decimal counterpart. a, 1, and d therefore become 10, 1, and 13 respectively. Number systems and bases. base systems like binary and hexadecimal seem a bit strange at first. the key is understanding how different systems “tick over” like an odometer when they are full. base 10, our decimal system, “ticks over” when it gets 10 items, creating a new digit. we wait 60 seconds before “ticking over” to a new minute. • the binary, hexadecimal, and octal number systems • finite representation of unsigned integers • finite representation of signed integers • finite representation of rational (floatingpoint) numbers why? • a power programmer must know number systems and data representation to fully understand c’s . primitive data types. primitive. T the octal number 122 to decimal. step 1: conver. the octal number to binary representation. we know that each octal digit takes3 binary di. ts. so for 122 octal, the ‘. becomes ‘001’, and each of the ‘2’s become. 010’. so 122 octal is now 001010010. step 2: convert the binary representation to decimal.

Number Systems Decimal Binary And Hexadecimal 1 Basen • the binary, hexadecimal, and octal number systems • finite representation of unsigned integers • finite representation of signed integers • finite representation of rational (floatingpoint) numbers why? • a power programmer must know number systems and data representation to fully understand c’s . primitive data types. primitive. T the octal number 122 to decimal. step 1: conver. the octal number to binary representation. we know that each octal digit takes3 binary di. ts. so for 122 octal, the ‘. becomes ‘001’, and each of the ‘2’s become. 010’. so 122 octal is now 001010010. step 2: convert the binary representation to decimal.

Comments are closed.