Nth Fibonacci Number Geeksforgeeks

Nth Fibonacci Number Geeksforgeeks The nth fibonacci number can be found using the golden ratio, which is approximately = [tex]\phi = \frac{1 \sqrt{5}}{2} [ tex]. the intuition behind this method is based on binet’s formula, which expresses the nth fibonacci number directly in terms of the golden ratio. Menu. back to explore page. given a positive integer n, find the nth fibonacci number.the fibonacci sequence is a sequence where the next term is the sum of the previous two terms. the first two terms of the fibonacci sequence are 0 followed by 1. the fibonacci sequ.
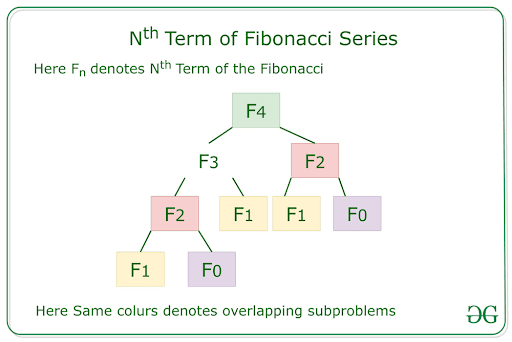
Nth Fibonacci Number Geeksforgeeks Given a number, find a representation of number as sum of non consecutive fibonacci numbers. examples: input: n = 10 output: 8 2 8 and 2 are two non consecutive fibonacci numbers and sum of them is 10. input: n = 30 output: 21 8 1 21, 8 and 1 are non consecutive fibonacci numbers and sum of them is 30. the idea is to use greedy algorithm. 1) let n. Read more: geeksforgeeks.org program for nth fibonacci number this video is contributed by anmol aggarwal.please like, comment and share the vide. The fibonacci numbers, commonly denoted f(n) form a sequence, called the fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. that is, f(0) = 0, f(1) = 1 f(n) = f(n 1) f(n 2), for n > 1. given n, calculate f(n). example 1: input: n = 2 output: 1 explanation: f(2) = f(1) f(0) = 1 0 = 1. A computer science portal for geeks. it contains well written, well thought and well explained computer science and programming articles, quizzes and practice competitive programming company interview questions.
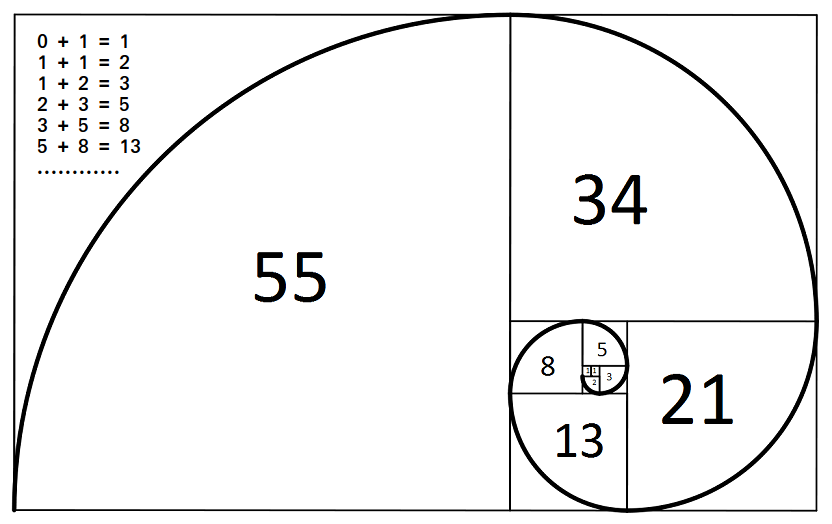
Program To Find And Print Nth Fibonacci Numbers Geeksforgeeks The fibonacci numbers, commonly denoted f(n) form a sequence, called the fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. that is, f(0) = 0, f(1) = 1 f(n) = f(n 1) f(n 2), for n > 1. given n, calculate f(n). example 1: input: n = 2 output: 1 explanation: f(2) = f(1) f(0) = 1 0 = 1. A computer science portal for geeks. it contains well written, well thought and well explained computer science and programming articles, quizzes and practice competitive programming company interview questions. The following recurrence relation defines the sequence f n of fibonacci numbers: f{n} = f{n 1} f{n 2} with base values f(0) = 0 and f(1) = 1. following is the naive implementation in c, java, and python for finding the nth member of the fibonacci sequence: we can easily convert the above recursive program into an iterative one. if we. I recently learned about using matrix multiplication to generate fibonacci numbers, which was pretty cool. you take a base matrix: [1, 1] [1, 0] and multiply it by itself n times to get: [f(n 1), f(n)] [f(n), f(n 1)] this morning, doodling in the steam on the shower wall, i realized that you could cut the running time in half by starting with.

Nth Fibonacci Number Geeksforgeeks 57 Off The following recurrence relation defines the sequence f n of fibonacci numbers: f{n} = f{n 1} f{n 2} with base values f(0) = 0 and f(1) = 1. following is the naive implementation in c, java, and python for finding the nth member of the fibonacci sequence: we can easily convert the above recursive program into an iterative one. if we. I recently learned about using matrix multiplication to generate fibonacci numbers, which was pretty cool. you take a base matrix: [1, 1] [1, 0] and multiply it by itself n times to get: [f(n 1), f(n)] [f(n), f(n 1)] this morning, doodling in the steam on the shower wall, i realized that you could cut the running time in half by starting with.

Comments are closed.