Non Stop Fibonacci Spiral

File Fibonacci Spiral Geogebra Svg Wikipedia Jun 29, 2023. it’s the most famous mathematical sequence in biology—the description of a spiral with a particular ratio found in the evolution of plants going back millions of years, and that. 2. sunflowers. (credit: kate babiy shutterstock) sunflowers are another famous example of fibonacci at work in nature. particularly, the arrangement of seedheads on sunflowers often takes on fibonacci numbers. for example, if 34 seed rows curve clockwise, then either 21 or 55 seed rows will spiral the other way.
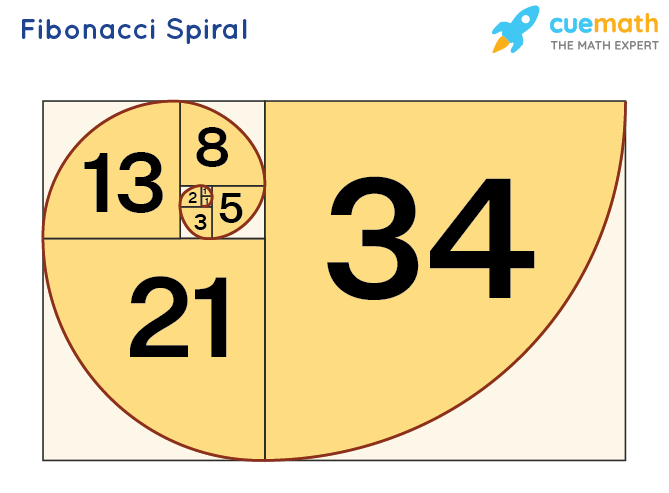
Fibonacci Sequence Formula Spiral Properties The fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio of each number in the fibonacci series to the one before it converges on phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively) fibonacci spirals and golden. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. It indicates that non fibonacci spirals were common in ancient clubmosses and that the evolution of leaf spirals diverged into two separate paths. the leaves of ancient clubmosses had an entirely distinct evolutionary history from the other major groups of plants today such as ferns, conifers, and flowering plants. spiral arranged leaves can be. A mountain aster may have 13 spirals to the left and 21 to the right. sunflowers are the most spectacular example, typically having 55 spirals one way and 89 in the other; or, in the finest varieties, 89 and 144. pine cones are also constructed in a spiral fashion, small ones having commonly with 8 spirals one way and 13 the other.

Fibonacci Spiral 34 Math Science History It indicates that non fibonacci spirals were common in ancient clubmosses and that the evolution of leaf spirals diverged into two separate paths. the leaves of ancient clubmosses had an entirely distinct evolutionary history from the other major groups of plants today such as ferns, conifers, and flowering plants. spiral arranged leaves can be. A mountain aster may have 13 spirals to the left and 21 to the right. sunflowers are the most spectacular example, typically having 55 spirals one way and 89 in the other; or, in the finest varieties, 89 and 144. pine cones are also constructed in a spiral fashion, small ones having commonly with 8 spirals one way and 13 the other. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034. In fact, non fibonacci spirals were the most common arrangement. the discovery of non fibonacci spirals in such an early fossil is surprising as they are very rare in living plant species today.

Comments are closed.