Newtons Method For Solving System Of Nonlinear Equations With 2 complex dynamics and newton’s method 2.1 newton’s method as we have said, newton’s method is an iterative algorithm for finding the roots of a di↵erentiable function. but before we define newton’s method precisely, let us make a few normalizing assumptions. in this paper, we will consider newton’s method applied specifically to. The newton raphson method of solving nonlinear equations. includes both graphical and taylor series derivations of the equation, demonstration of its applications, and discussions of its advantages ….
Newton S Method For System Of Non Linear Equations Youtube Ing systems of nonlinear equations. first, we will study newton’s method for solving multivariable nonlinear equations, which involves using the jacobian matrix. second, we will examine a quasi newton which is called broyden’s method; this method has been described as a generalization of the secant method. and third, to s solve for nonlin. The solutions are the same. linear systems have exactly zero, one, or infinitely many solutions. by contrast, nonlinear systems can have any number of solutions. the function f(x) = x2. 4 has two roots: x = 2 and x = 2. unlike linear systems, there is no grand solvability theorem for nonlinear systems. Newton’s method for systems of equations it is much harder if not impossible to do globally convergent methods like bisection in higher dimensions! a good initial guess is therefore a must when solving systems, and newton’s method can be used to re ne the guess. the basic idea behind newton’s method is to linearize the equation. J (x o) * d x = f (x o) this is a linear system of equations, so we can solve it for d x= (x x o). so here is newton's algorithm: 0) make an initial guess at the solution x. 1) evaluate j (x) and f (x) 2) solve j* d x = f. 3) x = x d x. 4) if for all k, |dx k | < rtol * |x k | atol we have converged. 5) if not, go back to step 1.
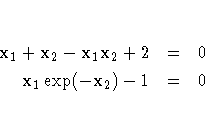
Example 8 2 Newton S Method For Solving Nonlinear Systems Of Equations Newton’s method for systems of equations it is much harder if not impossible to do globally convergent methods like bisection in higher dimensions! a good initial guess is therefore a must when solving systems, and newton’s method can be used to re ne the guess. the basic idea behind newton’s method is to linearize the equation. J (x o) * d x = f (x o) this is a linear system of equations, so we can solve it for d x= (x x o). so here is newton's algorithm: 0) make an initial guess at the solution x. 1) evaluate j (x) and f (x) 2) solve j* d x = f. 3) x = x d x. 4) if for all k, |dx k | < rtol * |x k | atol we have converged. 5) if not, go back to step 1. Fundamental insight into the solution of systems of nonlinear equations was provided by powell. it was found that newton iterations, with exact line searches, did not converge to a stationary point of the natural merit function, i.e., the euclidean norm of the residuals. extensive numerical simulation of powell’s equations produced the unexpected result that newton iterations converged to. Part viia: nonlinear equations newton’s method implementation of a newton iteration evaluate f(x c); terminate? solve f0(x c)s = f(x c) x = x c s you can write this at home! formulations of newton di er in the way they solve for s. c c. t. kelley, i. c. f. ipsen, 2016 part viia: nonlinear equations ma 580, fall 2016 15 75.
Comments are closed.