How To Multiply Polynomials Vertically Charles Lanier S This is where using the distributive property (or distributive method) will help you! to multiply these polynomials, start by taking the first polynomial (the purple monomial) and multiplying it by each term in the second polynomial (the green trinomial). this can be done by multiplying 4x^2 by the first term of the green trinomial (figure 1. This video sets up vertical multiplication and solves step by step. polynomials are multiplied in a variety of ways. this video sets up vertical multiplication and solves step by step.
5 Ways To Multiply Polynomials Wikihow Students learn how to multiply polynomials using the vertical method. 👉 learn how to multiply polynomials. to multiply polynomials, we use the distributive property. the distributive property is essential for multiplying polyn. Multiplying polynomials. a polynomial looks like this: example of a polynomial. this one has 3 terms. to multiply two polynomials: multiply each term in one polynomial by each term in the other polynomial. add those answers together, and simplify if needed. let us look at the simplest cases first. Example: multiply 5x 2 with 3y. step 1: we will first multiply the coefficients of both the polynomials i.e., 5 × 3= 15. step 2: since the above polynomials have two different variables, they cannot be multiplied. hence, we will keep them the same. the final answer is 5x 2 × 3y = 15x 2 y.
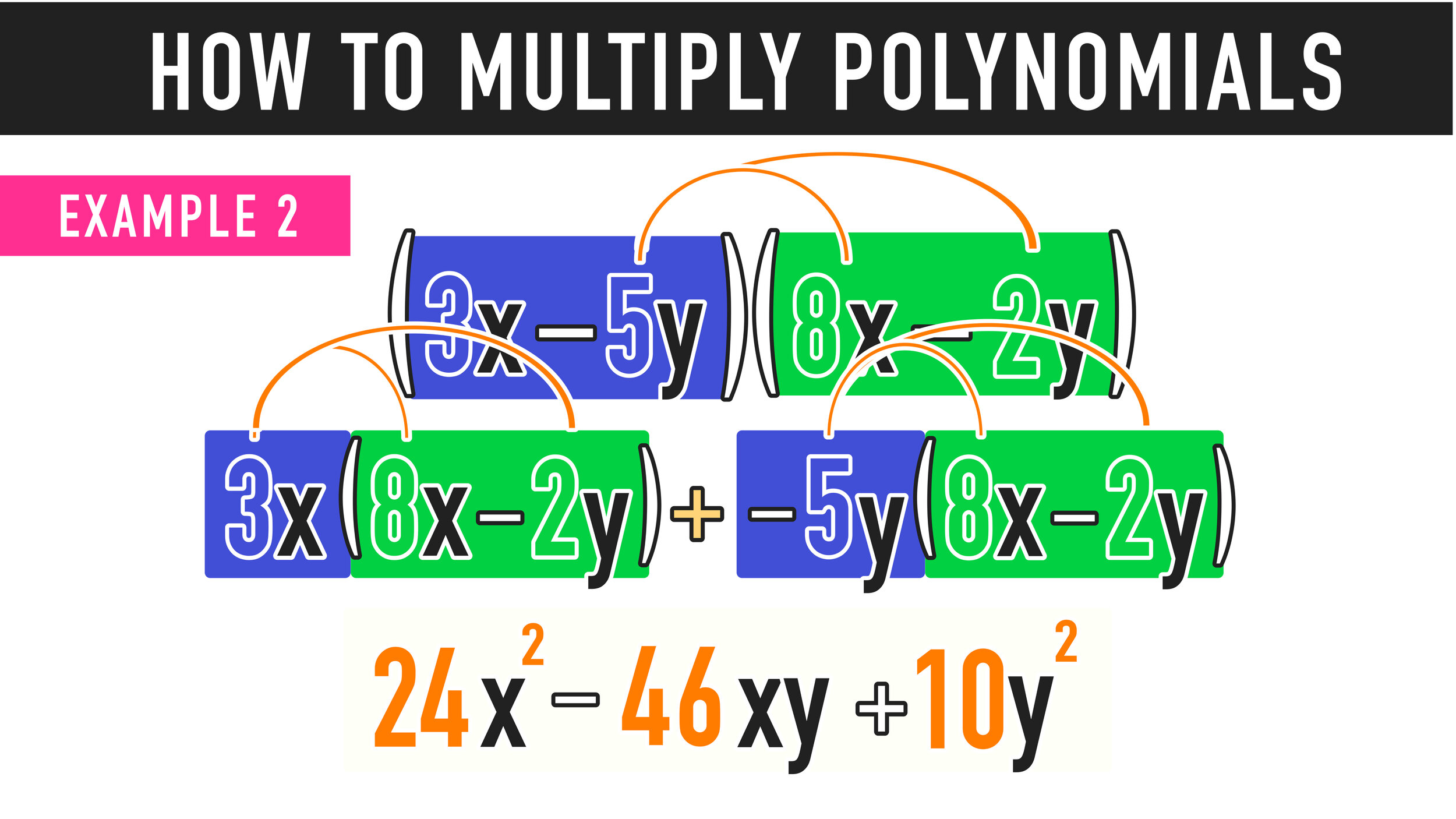
Multiplying Polynomials The Complete Guide Mashup Math Multiplying polynomials. a polynomial looks like this: example of a polynomial. this one has 3 terms. to multiply two polynomials: multiply each term in one polynomial by each term in the other polynomial. add those answers together, and simplify if needed. let us look at the simplest cases first. Example: multiply 5x 2 with 3y. step 1: we will first multiply the coefficients of both the polynomials i.e., 5 × 3= 15. step 2: since the above polynomials have two different variables, they cannot be multiplied. hence, we will keep them the same. the final answer is 5x 2 × 3y = 15x 2 y. Write the first binomial, x – 4 –4 vertically and the second binomial, x 2, horizontally. then multiply the corresponding terms and place the partial products in their individual square grid. now, add up all the terms inside the square grids. make sure to combine like terms which in this case the terms. finish this off by combining like. Multiply using the vertical method: (b 3)(2b2 − 5b 8) it is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way. multiply (2b2 − 5b 8) by 3. multiply (2b2 − 5b 8) by b. add like terms.
Comments are closed.