More Properties Of Exponents

All Properties Of Exponents More properties of exponents date period simplify. your answer should contain only positive exponents. 1) (x−2x−3) 4 1 x20 2) (x4) −3 ⋅ 2x4 2 x8 3) (n3) 3 ⋅ 2n−1 2n8 4) (2v)2 ⋅ 2v2 8v4 5) 2x2 y4 ⋅ 4x2 y4 ⋅ 3x 3x−3 y2 8x8y6 6) 2y3 ⋅ 3xy3 3x2 y4 2y2 x 7) x3 y3 ⋅ x3 4x2 x4y3 4 8) 3x2 y2 2x−1 ⋅ 4yx2 3xy 8 9) x. No way! we need a more sophisticated way in multiplying expressions with exponents. hence, taking a look at example 6.1.1 , we can see the result is \(a^5\). notice we could have obtained this answer without expanding but by simply adding the exponents: \[a^3\cdot a^2=a^{3 2}=a^5\nonumber\] this is called the product rule of exponents.

Properties Of Exponents Formula Examples Lesson Study Conclusion: formulas with exponents. throughout this post, we’ve explored various properties and rules of exponents, each simplifying the process of working with powers in different scenarios. here’s a quick recap of the key formulas: power of a product: (ab)^n = a^n \cdot b^n. multiplying exponents with the same base: a^m \times a^n = a^{m n}. What are the properties of exponents? the properties of exponents are some rules that we use while solving expressions that involve exponents. these rules help us to simplify expressions easily and quickly. a few important properties of exponents are listed below: a m × a n = a m n; a m a n = a m n; a 0 = 1; a m = 1 a m (a m) n = a mn (ab) m. Then we need to remind ourselves that when we raise a power to a power, we multiply the exponents. = 22(x5)2 (y3)2 raise each factor in the numerator and denominator to the second power. = 4x10 y6 simplify: 22 = 4, (x5)2 = x10, and (y3)2 = y6. you try 2.5.13. simplify: (a4 3b2)3. The exponent of the answer is the product of the exponents: (x2)3 = x2 ⋅ 3 = x6. in other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents. (am)n = am ⋅ n. be careful to distinguish between uses of the product rule and the power rule.

More Properties Of Exponents Then we need to remind ourselves that when we raise a power to a power, we multiply the exponents. = 22(x5)2 (y3)2 raise each factor in the numerator and denominator to the second power. = 4x10 y6 simplify: 22 = 4, (x5)2 = x10, and (y3)2 = y6. you try 2.5.13. simplify: (a4 3b2)3. The exponent of the answer is the product of the exponents: (x2)3 = x2 ⋅ 3 = x6. in other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents. (am)n = am ⋅ n. be careful to distinguish between uses of the product rule and the power rule. Rewriting roots as rational exponents. exponential equation with rational answer. rewriting mixed radical and exponential expressions. evaluating fractional exponents. evaluating fractional exponents: negative unit fraction. evaluating fractional exponents: fractional base. evaluating quotient of fractional exponents. Negative exponents are the reciprocals of the positive exponents. x−a = 1 xa, x ≠ 0 x − a = 1 x a, x ≠ 0. xa = 1 x−a, x ≠ 0 x a = 1 x − a, x ≠ 0. the same properties of exponents apply for both positive and negative exponents. in earlier chapters we talked about the square root as well. the square root of a number x is the same.
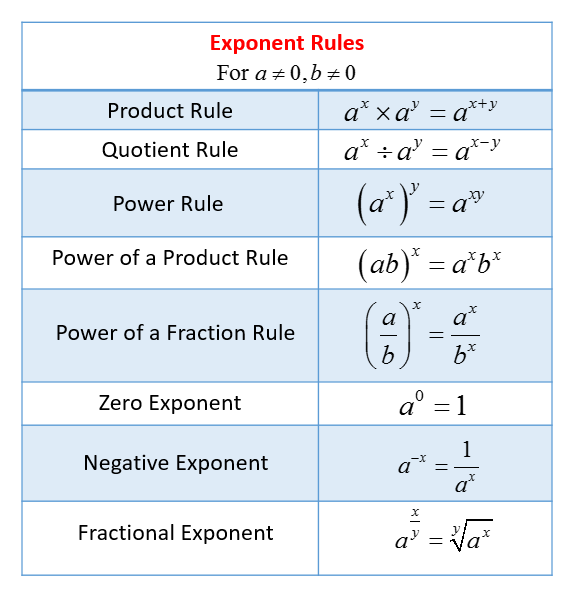
Exponents Exponential Notation And Scientific Notation Solutions Rewriting roots as rational exponents. exponential equation with rational answer. rewriting mixed radical and exponential expressions. evaluating fractional exponents. evaluating fractional exponents: negative unit fraction. evaluating fractional exponents: fractional base. evaluating quotient of fractional exponents. Negative exponents are the reciprocals of the positive exponents. x−a = 1 xa, x ≠ 0 x − a = 1 x a, x ≠ 0. xa = 1 x−a, x ≠ 0 x a = 1 x − a, x ≠ 0. the same properties of exponents apply for both positive and negative exponents. in earlier chapters we talked about the square root as well. the square root of a number x is the same.

Comments are closed.