Mean Of Grouped Data Using The Class Mark Method Statistics

Mean Of Grouped Data Using The Class Mark Method Statistics The three methods to find the mean of the grouped data is: direct method; assumed mean method; step deviation method. now, let us discuss all these three methods one by one. direct method. consider the same example as given above. now, convert the ungrouped data into grouped data by forming a class interval of width 15. How to find the mean of grouped data using the class mark method is explained in this video.

Mean Of A Grouped Data Igcse At Mathematics Realm There are two different formulas for calculating the mean for ungrouped data and the mean for grouped data. let us look at the formula to calculate the mean of grouped data. the formula is: x̄ = Σf i i n. where, x̄ = the mean value of the set of given data. f = frequency of the individual data. n = sum of frequencies. Grouped data to find the mean . a mean can be determined for grouped data, or data that is placed in intervals. unlike listed data, the individual values for grouped data are not available, and you are not able to calculate their sum. to calculate the mean of grouped data, the first step is to determine the midpoint (also called a class mark. To find mean using direct method, we can use the following steps: step 1: for each class, find the class mark xi, as. x=1 2 (lower limit upper limit) step 2: calculate fi.xi for each i. step 3: use the formula mean = ∑ (fi.xi) ∑fi. example: find the mean of the following data. class interval. Summary. for grouped data, we cannot find the exact mean, median and mode, we can only give estimates. to estimate the mean use the midpoints of the class intervals: estimated mean = sum of (midpoint × frequency) sum of frequency. to estimate the median use: estimated median = l (n 2) − b g × w. where:.

Assumed Mean Method For Grouped Data Class 10 Youtube To find mean using direct method, we can use the following steps: step 1: for each class, find the class mark xi, as. x=1 2 (lower limit upper limit) step 2: calculate fi.xi for each i. step 3: use the formula mean = ∑ (fi.xi) ∑fi. example: find the mean of the following data. class interval. Summary. for grouped data, we cannot find the exact mean, median and mode, we can only give estimates. to estimate the mean use the midpoints of the class intervals: estimated mean = sum of (midpoint × frequency) sum of frequency. to estimate the median use: estimated median = l (n 2) − b g × w. where:. The mean of grouped data using the class marks when the number of items in a set of data is too big, items are grouped for convenience. the manner of computing for the mean of grouped data is given by the formula: (fx) mean f ∑ = ∑ where: f is the frequency of each class x is the class mark of class. 2. in finding the sample mean for grouped data, we use the following formula: x¯ = ∑fx n x ¯ = ∑ f x n. where: x¯ x ¯ is the sample. f f is the frequency of a class. x x is the class mark. n n is the total frequency. why do we use the class mark for x x in grouped data, unlike in raw data where x x is the value of the data?.

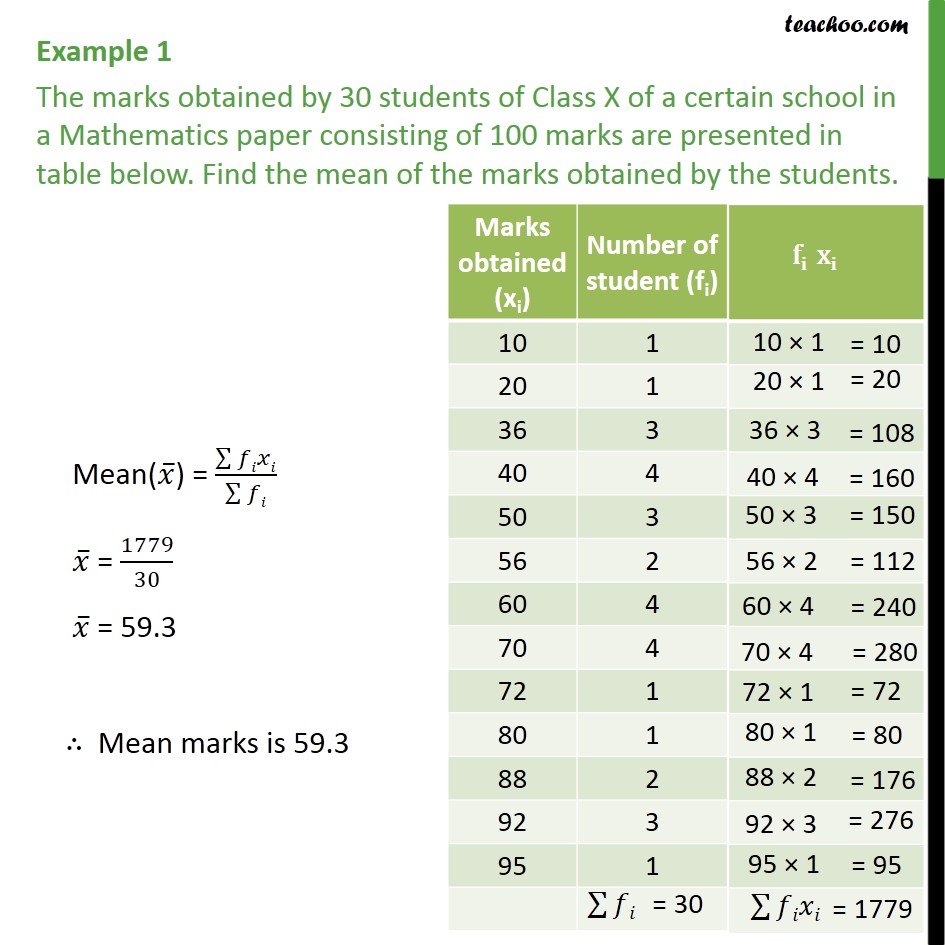
Example 1 The Marks Obtained By 30 Students Of Class X The mean of grouped data using the class marks when the number of items in a set of data is too big, items are grouped for convenience. the manner of computing for the mean of grouped data is given by the formula: (fx) mean f ∑ = ∑ where: f is the frequency of each class x is the class mark of class. 2. in finding the sample mean for grouped data, we use the following formula: x¯ = ∑fx n x ¯ = ∑ f x n. where: x¯ x ¯ is the sample. f f is the frequency of a class. x x is the class mark. n n is the total frequency. why do we use the class mark for x x in grouped data, unlike in raw data where x x is the value of the data?.