Mean Deviation Definition Formula Examples And Faqs

Mean Deviation Definition Formula Examples And Faqs Step 4: find the sum of all the deviations and divide it by the number of observations to get the mean deviation. this can be understood using the example, example: find the mean deviation of the given data about their mean. {4, 6, 7, 3, 5, 5} solution: step 1: find the mean of the given data. Mean deviation formula for grouped data. when data is organized and classified into groups it is known as grouped data. grouping of data is done by continuous and discrete frequency distributions. the mean deviation formulas for grouped data are given below: mean deviation for continuous frequency distribution. such a type of grouped data.
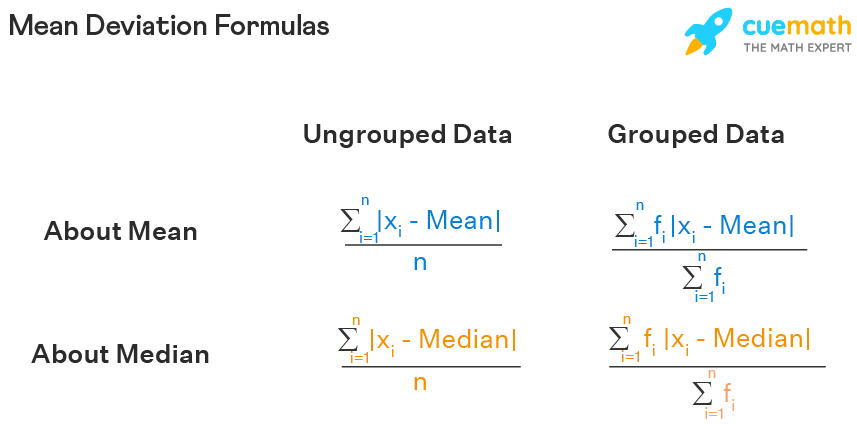
Mean Deviation Formula Definition Meaning Examples Definition; formula; mean deviation for frequency distribution; examples; faqs; mean deviation definition. the mean deviation is defined as a statistical measure that is used to calculate the average deviation from the mean value of the given data set. the mean deviation of the data values can be easily calculated using the below procedure. 3) continuous series: the formula to find the mean deviation from mode for a continuous series is: md=\[\frac{\sum f\mid x {mode}\mid}{\sum f}\] ∑ = summation. x = mid value of the class . m = mode. f = frequency of observations. mean deviation examples. example 1) calculate the mean deviation and the coefficient of mean deviation using the. Mean deviation formula. the mean deviation is the mean of the absolute deviations of the observations or values from a suitable average. this suitable average may be the mean, median or mode. we also know it as the mean absolute deviation. the basic formula to calculate mean deviation for a given data set is as follows: where,. Frequently asked questions on mean deviation formula. here are some of the most common faqs on mean deviation formula and definition: q1: how do we calculate the mean deviation? ans: follow the steps mentioned below to calculate the mean deviation: step \(1\): find the mean or the average value for the given data values.

Mean Deviation Formula Learn Formula For Mean Deviation Mean deviation formula. the mean deviation is the mean of the absolute deviations of the observations or values from a suitable average. this suitable average may be the mean, median or mode. we also know it as the mean absolute deviation. the basic formula to calculate mean deviation for a given data set is as follows: where,. Frequently asked questions on mean deviation formula. here are some of the most common faqs on mean deviation formula and definition: q1: how do we calculate the mean deviation? ans: follow the steps mentioned below to calculate the mean deviation: step \(1\): find the mean or the average value for the given data values. Definition; formula; mean deviation for frequency distribution; examples; faqs; mean deviation definition. the mean deviation is defined as a statistical measure that is used to calculate the average deviation from the mean value of the given data set. the mean deviation of the data values can be easily calculated using the below procedure. A mean deviation is a statistical approach to determine the average deviation of values from the mean in an example. it is calculated first by obtaining the average of the observations. the difference of each observation from the mean is then defined and lastly, the mean deviation is determined through the formula.
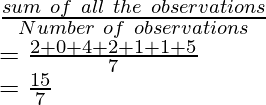
Mean Deviation Definition Formula Examples And Faqs Definition; formula; mean deviation for frequency distribution; examples; faqs; mean deviation definition. the mean deviation is defined as a statistical measure that is used to calculate the average deviation from the mean value of the given data set. the mean deviation of the data values can be easily calculated using the below procedure. A mean deviation is a statistical approach to determine the average deviation of values from the mean in an example. it is calculated first by obtaining the average of the observations. the difference of each observation from the mean is then defined and lastly, the mean deviation is determined through the formula.

Comments are closed.