Maximum Likelihood Estimation For Linear Regression Quantstart

Maximum Likelihood Estimation For Linear Regression Quantstart This is a conditional probability density (cpd) model. linear regression can be written as a cpd in the following manner: p (y ∣ x, θ) = (y ∣ μ (x), σ 2 (x)) for linear regression we assume that μ (x) is linear and so μ (x) = β t x. we must also assume that the variance in the model is fixed (i.e. that it doesn't depend on x) and as. The most popular method to do this is via ordinary least squares (ols). if we define the residual sum of squares (rss), which is the sum of the squared differences between the outputs and the linear regression estimates: rss (β) = ∑ i = 1 n (y i − f (x i)) 2 = ∑ i = 1 n (y i − β t x i) 2.
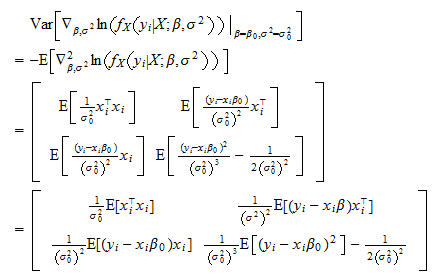
Linear Regression Maximum Likelihood Estimation The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is. Quantstart new york city october 2016 trip report. maximum likelihood estimation for linear regression. bayesian linear regression models with pymc3. Ml is a higher set of estimators which includes least absolute deviations (l1 l 1 norm) and least squares (l2 l 2 norm). under the hood of ml the estimators share a wide range of common properties like the (sadly) non existent break point. in fact you can use the ml approach as a substitute to optimize a lot of things including ols as long as. Properties of mle. maximum likelihood estimator : = arg max. best explains data we have seen. does not attempt to generalize to data not yet observed. often used when sample size is large relative to parameter space. potentially biased (though asymptotically less so, as → ∞) consistent: lim 9 − < = 1 where > 0. f.
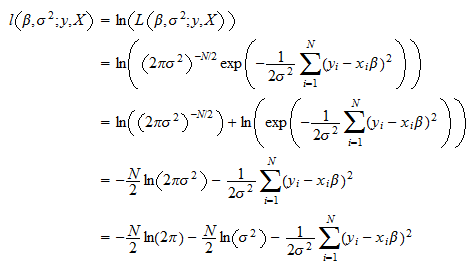
Linear Regression Maximum Likelihood Estimation Ml is a higher set of estimators which includes least absolute deviations (l1 l 1 norm) and least squares (l2 l 2 norm). under the hood of ml the estimators share a wide range of common properties like the (sadly) non existent break point. in fact you can use the ml approach as a substitute to optimize a lot of things including ols as long as. Properties of mle. maximum likelihood estimator : = arg max. best explains data we have seen. does not attempt to generalize to data not yet observed. often used when sample size is large relative to parameter space. potentially biased (though asymptotically less so, as → ∞) consistent: lim 9 − < = 1 where > 0. f. Estimation (mle). maximum likelihood estimation is a cornerstone of statistics and it has many wonderful properties that are out of scope for this course. at the end of the day, however, we can think of this as being a different (negative) loss function: µ! = µmle = argmax µ pr({y n}n n=1 | µ,σ 2) = argmax µ #n n=1 1 σ √ 2π exp! −. One widely used alternative is maximum likelihood estimation, which involves specifying a class of distributions, indexed by unknown parameters, and then using the data to pin down these parameter values. the benefit relative to linear regression is that it allows more flexibility in the probabilistic relationships between variables.
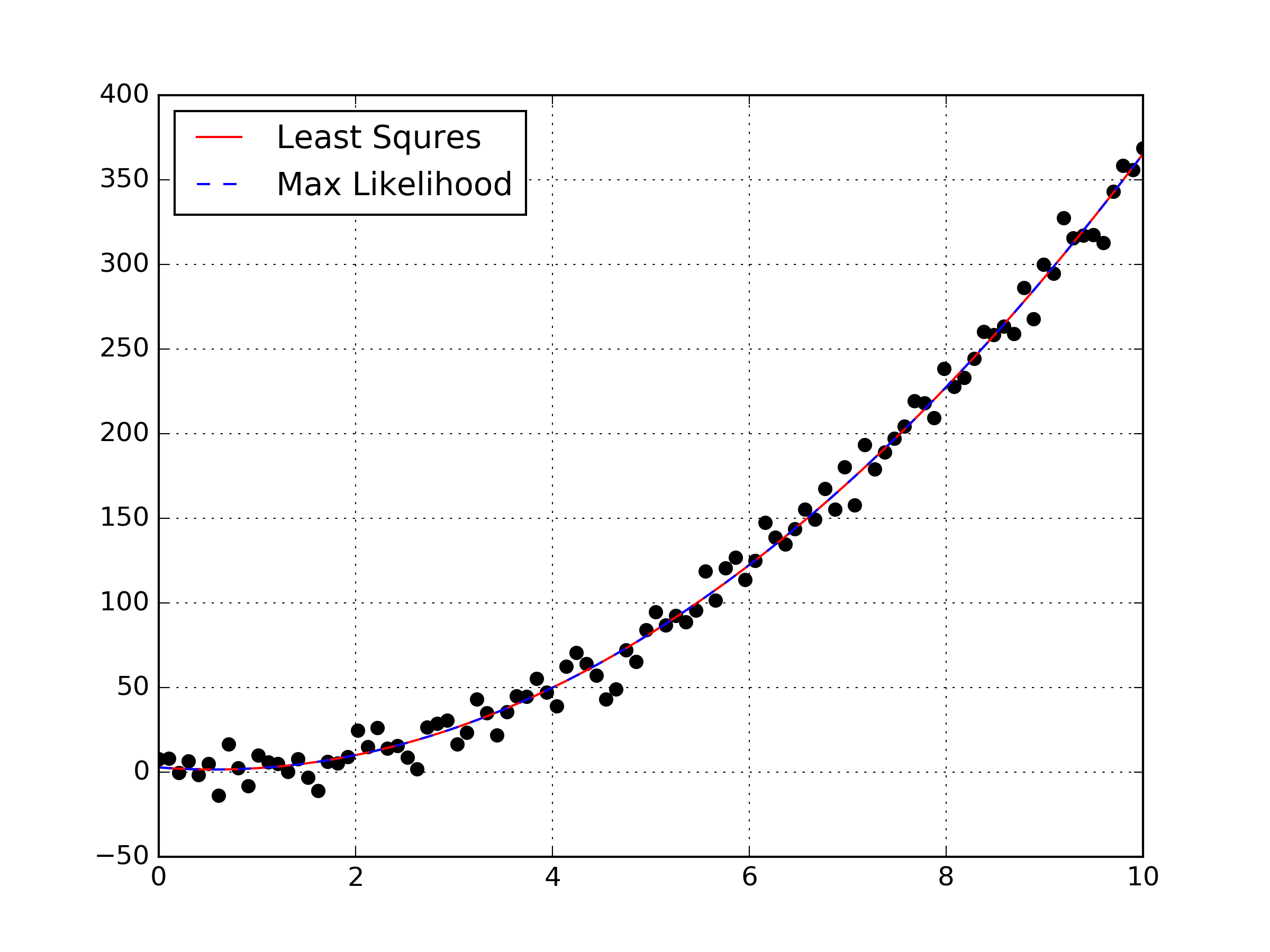
Charles Jekel Jekel Me Maximum Likelihood Estimation Linear Regression Estimation (mle). maximum likelihood estimation is a cornerstone of statistics and it has many wonderful properties that are out of scope for this course. at the end of the day, however, we can think of this as being a different (negative) loss function: µ! = µmle = argmax µ pr({y n}n n=1 | µ,σ 2) = argmax µ #n n=1 1 σ √ 2π exp! −. One widely used alternative is maximum likelihood estimation, which involves specifying a class of distributions, indexed by unknown parameters, and then using the data to pin down these parameter values. the benefit relative to linear regression is that it allows more flexibility in the probabilistic relationships between variables.

Introduction To Maximum Likelihood Estimation Youtube

Comments are closed.