Mathematics For Blondes Decision Of Unsolvable Equations
Mathematics For Blondes Decision Of Unsolvable Equations Decision of the first unsolvable equation x 2 = x this equation traditionally can be taken to next equality 2 = 0 as this equality did not look wildly, but in mathematics such quite possible. i will say anymore, the first equation is only one equation from the system of two equations, that has one common decision. the second equation looks so:. This witch doctor of mathematics profoundly gave out a page under the name "decision of unsolvable equalizations". according to his opinion, there is other task in that asked, how many hedgehogs will turn out, if to two hedgehogs to add the unknown amount of grass snakes. he assures that both tasks have an identical decision :))).

Mathematics For Blondes Decision Of Unsolvable Equations Sooner or later, the postulates are replaced by physical laws. temporary postulates physicists do not go to any comparison with the monumental firmness axioms of mathematics. here and there is a very sudden decision hilbert's sixth problem the language of mathematics is much easier to state "axioms" of religion than the axioms of physics. 1. when you have an equal number of equations and unknowns, put the coefficients on the variables into a matrix and take the determinant of the matrix. if the determinant does not equal zero, the system is solvable. if it does equal zero, it is not uniquely solvable. – hanzy. Equations are just abstract versions of phrasing a statement, so i wouldn't get hung up on that part. many of those famous unsolved equations can be phrased in plain language, like the collatz conjecture: so here's how it goes: pick a number, any number. if it's even, divide it by 2. if it's odd, multiply it by 3 and add 1. Some of these equations are even based on elementary school concepts and are easily understandable just unsolvable. 1. the riemann hypothesis. equation: σ (n) ≤ hn ln (hn)ehn. where n is a positive integer. hn is the n th harmonic number. σ (n) is the sum of the positive integers divisible by n.

Unsolvable Equations Algebra School Yourself Equations are just abstract versions of phrasing a statement, so i wouldn't get hung up on that part. many of those famous unsolved equations can be phrased in plain language, like the collatz conjecture: so here's how it goes: pick a number, any number. if it's even, divide it by 2. if it's odd, multiply it by 3 and add 1. Some of these equations are even based on elementary school concepts and are easily understandable just unsolvable. 1. the riemann hypothesis. equation: σ (n) ≤ hn ln (hn)ehn. where n is a positive integer. hn is the n th harmonic number. σ (n) is the sum of the positive integers divisible by n. The number of unit arcs and numbers is determined by formula (1). the number 6 is located on the continuation of the 2 ray and is the result of multiplying the number 2 by the number 3. calculations for 3 spiral. the 3.2 turn is formed by eighteen single arcs of size 20°, on which the numbers 9 to 26 are located. Many mathematical problems have been stated but not yet solved. these problems come from many areas of mathematics, such as theoretical physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and euclidean geometries, graph theory, group theory, model theory, number theory, set theory, ramsey theory, dynamical systems, and partial differential equations.

Unsolvable Equations School Yourself Algebra Pbs Learningmedia The number of unit arcs and numbers is determined by formula (1). the number 6 is located on the continuation of the 2 ray and is the result of multiplying the number 2 by the number 3. calculations for 3 spiral. the 3.2 turn is formed by eighteen single arcs of size 20°, on which the numbers 9 to 26 are located. Many mathematical problems have been stated but not yet solved. these problems come from many areas of mathematics, such as theoretical physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and euclidean geometries, graph theory, group theory, model theory, number theory, set theory, ramsey theory, dynamical systems, and partial differential equations.

Mathematics For Blondes Unsolvable Equalizations Are In Preschool
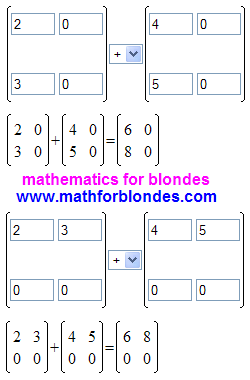
Mathematics For Blondes Matrix In Mathematics

Comments are closed.