Magic Square Examples 3×3
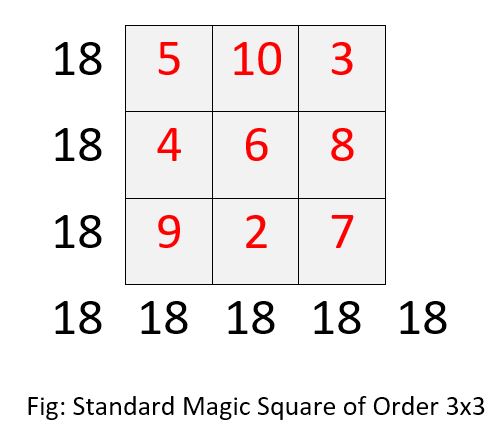
Magic Square Examples 3x3 To find the magic constant (s) for a normal magic square use the formula where equals the order, or number of rows, in the magic square. so for a 3×3 magic square, the formula would be: [2] s =. s =. s =. s =. s = 15. all rows, columns, and diagonals must add up to 15. For example, solving a 4 x 4 magic square is more complicated than solving a 3 x 3 square. we will focus on how to solve a 3 x 3 magic square , as it is the most straightforward version to solve.

Magic Square 3 X 3 Myworldtheirway Math Tricks How to solve magic square. as mentioned above, the formula of the magic square sum is n (n2 1) 2. for a magic square of order 3, we need to substitute n = 3 to know the magic sum so that we can easily form the magic square 3×3. when n = 3, the sum = 3 (3 2 1) = 3 (9 1) 2 = (3 × 10) 2 = 15. now, we have to place the numbers in the. The constant values m m of the sums of the magic squares have a minimum value (for non zero integer positive values). m =n(n2 1) 2 m = n (n 2 1) 2. for a size 3x3, the minimum constant is 15, for 4x4 it is 34, for 5x5 it is 65, 6x6 it is 111, then 175, 260, …. any lower sum will force the use of either negative numbers or fractions (not. For a 3x3 magic square, there is actually only one normal solution and all of the puzzles are derived from rotations or reflections of that puzzle. the normal variations of these puzzles (the 3x3 puzzles that contain only 1 9) will have a magic constant of 15. this should make solving the early puzzle worksheets pretty easy. Magic squares: a detailed strategy guide . by sylvie wilson. magic squares are simple to explain, yet they can easily lead to hours of fun mathematical explorations. for those of you who are new to the magic squares problem, the idea is this: given n greater than or equal to 3, can you find an n by n grid of n^2 consecutive numbers where all.

Solving A 3x3 Magic Square Overview Formula Examples Lesson For a 3x3 magic square, there is actually only one normal solution and all of the puzzles are derived from rotations or reflections of that puzzle. the normal variations of these puzzles (the 3x3 puzzles that contain only 1 9) will have a magic constant of 15. this should make solving the early puzzle worksheets pretty easy. Magic squares: a detailed strategy guide . by sylvie wilson. magic squares are simple to explain, yet they can easily lead to hours of fun mathematical explorations. for those of you who are new to the magic squares problem, the idea is this: given n greater than or equal to 3, can you find an n by n grid of n^2 consecutive numbers where all. The common sum along each of these lines is. s = 3(u^2 v^2) = 3(r^2 s^2) = 3[(a^2 b^2)(x^2 y^2)]^2. any magic square of squares whose central element is a sum of two. squares in no more than four ways must consist of some arrangement. of the four pairs of opposite terms shown in the square above, but. The reason there are only these 3x3 magic squares is simple enough. first of all, since. each row must add up to the same number, there are three rows, and. 1 2 3 4 5 6 7 8 9 is 45, each row must add up to 45 3, that is, 15. next, if you add the two diagonals and the middle column, you'll get 15 15 15=45 again.

Solving A 3x3 Magic Square Overview Formula Examples Video 57 Off The common sum along each of these lines is. s = 3(u^2 v^2) = 3(r^2 s^2) = 3[(a^2 b^2)(x^2 y^2)]^2. any magic square of squares whose central element is a sum of two. squares in no more than four ways must consist of some arrangement. of the four pairs of opposite terms shown in the square above, but. The reason there are only these 3x3 magic squares is simple enough. first of all, since. each row must add up to the same number, there are three rows, and. 1 2 3 4 5 6 7 8 9 is 45, each row must add up to 45 3, that is, 15. next, if you add the two diagonals and the middle column, you'll get 15 15 15=45 again.

How To Do A 3x3 Magic Square Amazing Trick Youtube
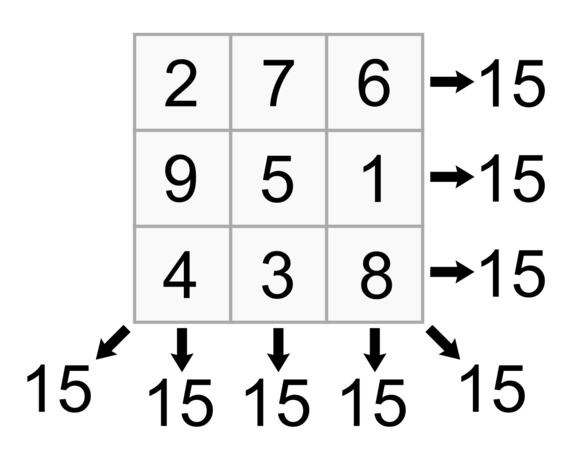
Winning Algorithm For Tic Tac Toe Using A 3x3 Magic Square

Comments are closed.