Load Distribution Types Structural Beam Types Uniformly Distributed

Vetor De Load Distribution Types Structural Beam Types Uniformly A uniformly distributed load (udl) is an action (load) on a structural element such as a beam, slab or column which has the same value at any point. in general, there are. uniformly distributed line loads and. uniformly distributed area loads. examples of this load would be snow, wind, live or dead load. but an image explains it much better. A uniformly distributed load can be represented mathematically as a constant value per unit length, typically denoted as 'w' in equations. the total load from a udl acting over a beam can be calculated by multiplying the load intensity by the length over which it acts. in structural analysis, udls simplify calculations for reactions at supports.

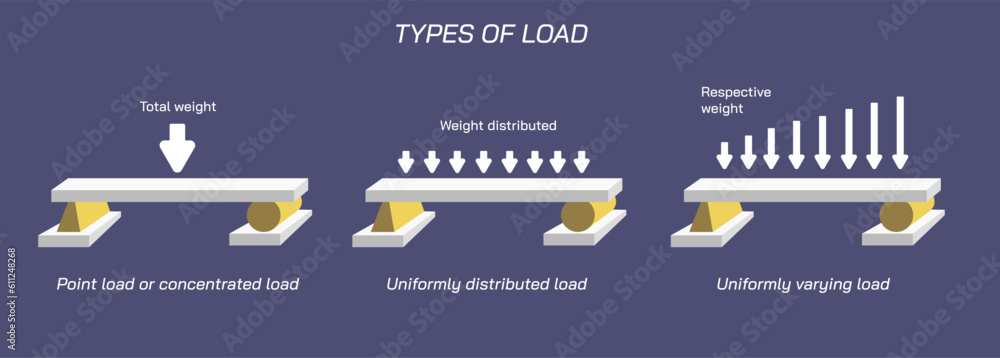
4 2 Common Load Types For Beams And Frames Learn About Structures The load travels through the slab and to both beams. the area load turns into a line load applied to the beams, calculated as area load ⋅ beam spacing 2. the load travels through the beams and to the columns. the line load of the beam turns into point loads applied axially on the columns. these are the reaction forces of the beam and. Arch 331 169 of note set 8.2 su2015abn. 1. simple beam— shear uniformly distributed load total equiv. uniform load w w12 wx 5 w14 384 el x) 4. m max. simple beam— shear uniform load partially ri = vi max. when a < c ra = va max. when a > c when x a and < m max. at x distributed (2c b) 21 21 ri —w (x—a). 3.3.1 intensity. distributed loads are a way to represent a force over a certain distance. sometimes called intensity, given the variable: intensity w = f d [=] n m, lb ft. while pressure is force over area (for 3d problems), intensity is force over distance (for 2d problems). it’s like a bunch of mattresses on the back of a truck. A uniformly distributed load is a load which has the same value everywhere, i.e. \(w(x) = c\text{,}\) a constant (a) a shelf of books with various weights. (b) each book represented as an individual weight (c) all the books represented as a distributed load. figure 7.8.1. we can use the computational tools discussed in the previous chapters to.

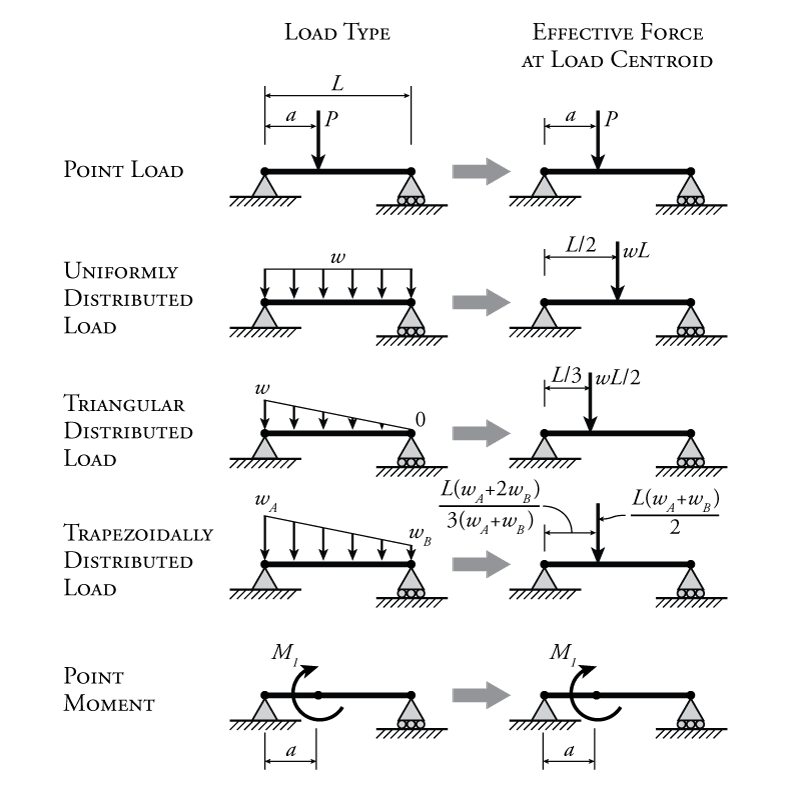
Load Distribution Types Structural Beam Types Uniformly Distributed 3.3.1 intensity. distributed loads are a way to represent a force over a certain distance. sometimes called intensity, given the variable: intensity w = f d [=] n m, lb ft. while pressure is force over area (for 3d problems), intensity is force over distance (for 2d problems). it’s like a bunch of mattresses on the back of a truck. A uniformly distributed load is a load which has the same value everywhere, i.e. \(w(x) = c\text{,}\) a constant (a) a shelf of books with various weights. (b) each book represented as an individual weight (c) all the books represented as a distributed load. figure 7.8.1. we can use the computational tools discussed in the previous chapters to. These uniform loads are given in units of force per unit distance (for example kn m). in addition to the uniform load, load may be distributed on structural members in other ways, such as the triangular or trapezoidal distributed loads shown in figure 4.1 (among others). we will also encounter point moments as shown in the figure. Moment loads can be created by offset forces or by external moments applied to the beam; uniformly and non uniformly distributed loads. distributed loads are forces applied over a length of the beam, either uniformly or non uniformly distributed the intensity of a distributed load is measured in force per unit length (q = f l) (q = \frac{f}{l.

Load Distribution Types Structural Beam Types Uniformly Distributed These uniform loads are given in units of force per unit distance (for example kn m). in addition to the uniform load, load may be distributed on structural members in other ways, such as the triangular or trapezoidal distributed loads shown in figure 4.1 (among others). we will also encounter point moments as shown in the figure. Moment loads can be created by offset forces or by external moments applied to the beam; uniformly and non uniformly distributed loads. distributed loads are forces applied over a length of the beam, either uniformly or non uniformly distributed the intensity of a distributed load is measured in force per unit length (q = f l) (q = \frac{f}{l.