Linear Systems With Infinite Solutions Example 2 Video Algebra

Linear Systems With Infinite Solutions Example 2 Video Algebra A system of equations in 3 variables will have infinite solutions if the planes intersect in an entire line or in an entire plane. the latter case occurs if all three equations are equivalent and represent the same plane. here is an example of the second case: x y z = 1. 2x 2y 2z = 2. 3x 3y 3z = 3. Key idea 1.4.1: consistent solution types. a consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. if a consistent linear system of equations has a free variable, it has infinite solutions. if a consistent linear system has more variables than leading 1s, then.

How To Solve A Linear System In Three Variables With No Or Infinite You'll also have systems with no solutions. but some systems have infinite solutions. how can systems have infinite solutions? if you solve a system with graphing, you might notice that the solution is where the lines cross. let's look at a system of equations that has infinite solutions: 22x 11y=4414x 7y=28 . try simplifying the top equation. The system of equations is: in this case it seems easiest to set them equal to each other: d = 0.2t = 0.5 (t−6) start with: 0.2t = 0.5 (t − 6) expand 0.5 (t−6): 0.2t = 0.5t − 3. subtract 0.5t from both sides: −0.3t = −3. divide both sides by −0.3: t = −3 −0.3 = 10 minutes. now we know when you get caught!. Algebra 1. course: algebra 1 > unit 6. lesson 5: number of solutions to systems of equations. systems of equations number of solutions: fruit prices (1 of 2) systems of equations number of solutions: fruit prices (2 of 2) solutions to systems of equations: consistent vs. inconsistent. solutions to systems of equations: dependent vs. independent. Case iii: infinite solutions. this is the rarest case and only occurs when you have the same line. consider, for instance, the two lines below (y = 2x 1 and 2y = 4x 2). these two equations are really the same line. example of a system that has infinite solutions: line 1: y = 2x 1. line 2: 2y = 4x 2.
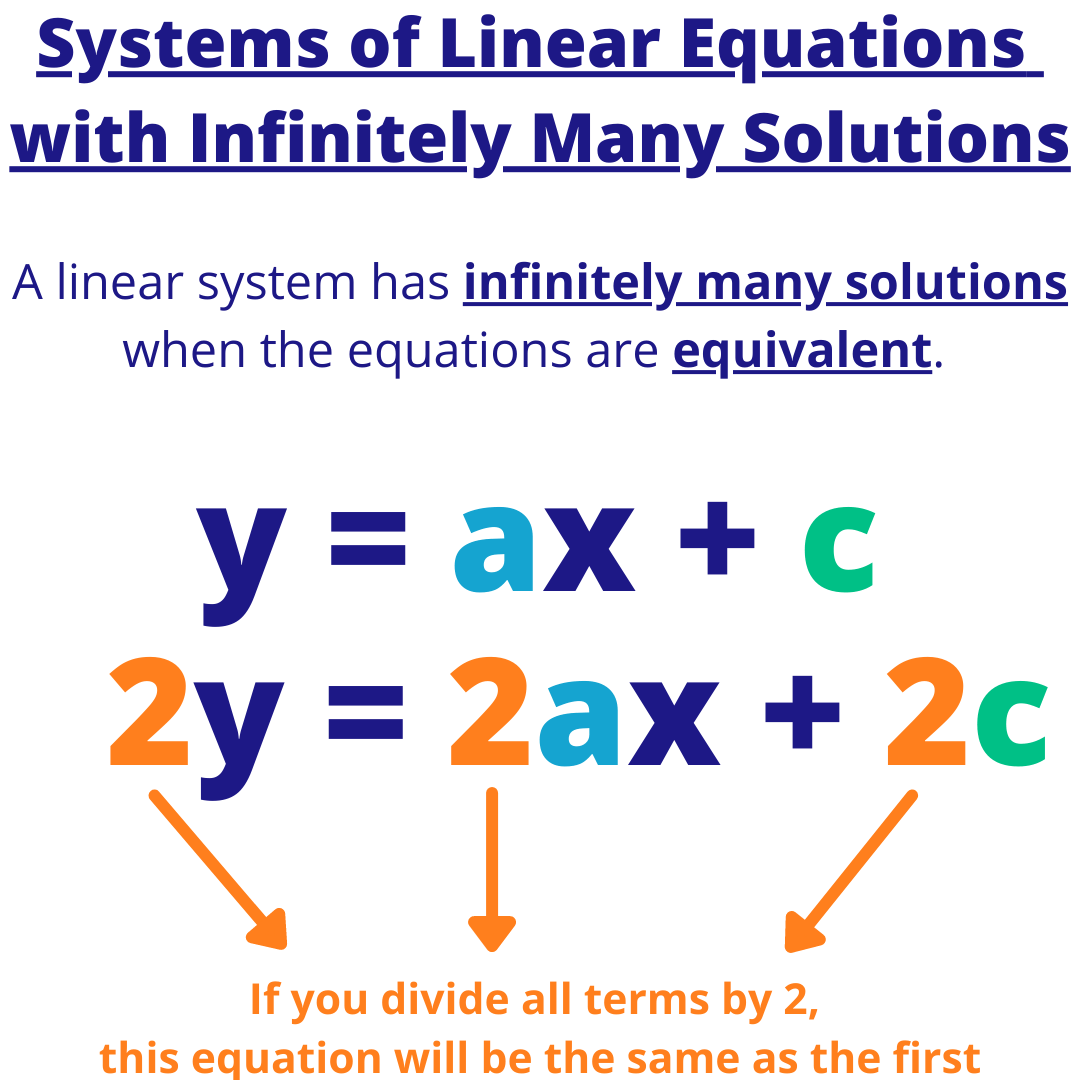
Systems Of Linear Equations With Infinite Solutions Examples Expii Algebra 1. course: algebra 1 > unit 6. lesson 5: number of solutions to systems of equations. systems of equations number of solutions: fruit prices (1 of 2) systems of equations number of solutions: fruit prices (2 of 2) solutions to systems of equations: consistent vs. inconsistent. solutions to systems of equations: dependent vs. independent. Case iii: infinite solutions. this is the rarest case and only occurs when you have the same line. consider, for instance, the two lines below (y = 2x 1 and 2y = 4x 2). these two equations are really the same line. example of a system that has infinite solutions: line 1: y = 2x 1. line 2: 2y = 4x 2. Recognize when the solution to a system of linear equations implies there are an infinite number of solutions solve a system of equations using the substitution method in the last couple sections, we verified that ordered pairs were solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. 2. any solution to this system of equations must then have z = 2. z = 2. once we know that, we may substitute z = 2 z = 2. into the first and second equation and simplify to obtain a new system of equations having the same solutions: − x 2y = − 1 3y = − 3. z = 2. − x 2 y 3 y z = = = − 1 − 3. 2.

Simple Ways To Solve Equations With Infinite Solutions Recognize when the solution to a system of linear equations implies there are an infinite number of solutions solve a system of equations using the substitution method in the last couple sections, we verified that ordered pairs were solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. 2. any solution to this system of equations must then have z = 2. z = 2. once we know that, we may substitute z = 2 z = 2. into the first and second equation and simplify to obtain a new system of equations having the same solutions: − x 2y = − 1 3y = − 3. z = 2. − x 2 y 3 y z = = = − 1 − 3. 2.

Comments are closed.