Linear Regression 101 Part 3 Assumptions Evaluation Standard

Linear Regression 101 Part 3 Assumptions Evaluation Standard Linear regression 101 (part 3 assumptions & evaluation) 11 minute read introduction. we covered tha basics of linear regression in part 1 and key model metrics were explored in part 2. now we’re ready to tackle the basic assumptions of linear regression, how to investigate whether those assumptions are met, and how to address key problems. In the case of a linear regression model, these are called the assumptions’, which must hold for a linear regression framework to apply to any data. below is the laundry list of all assumptions of a linear regression model. please note that 1–6 are the key ones and 7–10 would be derived or more implicit. linearity in parameters.

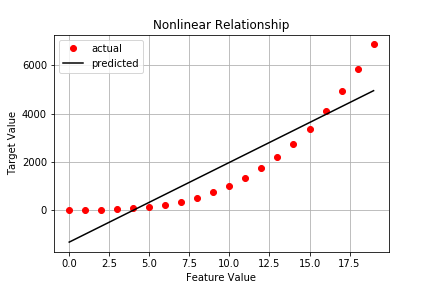
Linear Regression 101 Part 3 Assumptions Evaluation Standard However, before we conduct linear regression, we must first make sure that four assumptions are met: 1. linear relationship: there exists a linear relationship between the independent variable, x, and the dependent variable, y. 2. independence: the residuals are independent. in particular, there is no correlation between consecutive residuals. 16.1.1 ordinary least squares. regression analysis is a broad class of analytic techniques. what we’ve practiced in the last few chapters is a specific type of regression, specifically ordinary least squares (ols). it’s called ordinary least squares because the coefficients in an ols regression are chosen by the principle of least squares. 1.3. what happens when the linearity assumption is violated. when this assumption is violated, we may get: biased regression coefficients; biased standard errors; biased p values; biased r 2; so linearity is the most important linear regression assumption since its violation biases all the model’s output. 1.4. how to deal with non linearity. Let’s interpret the results for the following multiple linear regression equation: air conditioning costs$ = 2 * temperature c – 1.5 * insulation cm. the coefficient sign for temperature is positive ( 2), which indicates a positive relationship between temperature and costs.

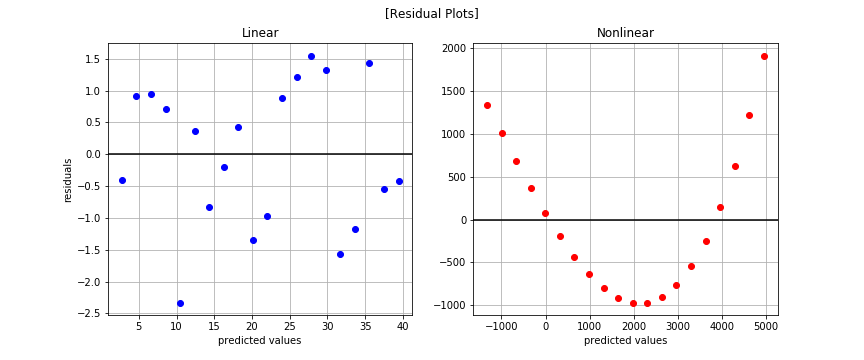
Linear Regression 101 Part 3 Assumptions Evaluation Standard 1.3. what happens when the linearity assumption is violated. when this assumption is violated, we may get: biased regression coefficients; biased standard errors; biased p values; biased r 2; so linearity is the most important linear regression assumption since its violation biases all the model’s output. 1.4. how to deal with non linearity. Let’s interpret the results for the following multiple linear regression equation: air conditioning costs$ = 2 * temperature c – 1.5 * insulation cm. the coefficient sign for temperature is positive ( 2), which indicates a positive relationship between temperature and costs. In linear regression, the additivity assumption simply says that when there are multiple variables, their total influence on the outcome is best stated by combining their effects together (i.e., the effect of each predictor variable on the outcome variable is additive and independent of other predictors). for a multiple linear regression model. The first assumption of linear regression is the independence of observations. independence means that there is no relation between the different examples. this is not something that can be deduced by looking at the data: the data collection process is more likely to give an answer to this.

Linear Regression 101 Part 3 Assumptions Evaluation Standard In linear regression, the additivity assumption simply says that when there are multiple variables, their total influence on the outcome is best stated by combining their effects together (i.e., the effect of each predictor variable on the outcome variable is additive and independent of other predictors). for a multiple linear regression model. The first assumption of linear regression is the independence of observations. independence means that there is no relation between the different examples. this is not something that can be deduced by looking at the data: the data collection process is more likely to give an answer to this.

Linear Regression 101 Part 3 Assumptions Evaluation Standard