Lets Get To Know The Pythagorean Theorem Step By Step

Let S Get To Know The Pythagorean Theorem Step By Step Youtube Tabletclass math: tcmathacademy math help with the pythagorean theorem. for more math help to include math lessons, practice problems and math tu. Use the pythagorean theorem to determine the length of x. step 1. identify the legs and the hypotenuse of the right triangle. the legs have length 6 and 8. x x is the hypotenuse because it is opposite the right angle. step 2. substitute values into the formula (remember 'c' is the hypotenuse). a2 b2 = c2 62 82 = x2 a 2 b 2 = c 2 6 2 8 2.

How To Prove The Pythagorean Theorem 10 Steps With Pictures What is the pythagorean theorem? the pythagorean theorem states that the square of the longest side of a right triangle (called the hypotenuse) is equal to the sum of the squares of the other two sides. pythagorean theorem formula shown with triangle abc is: a^2 b^2=c^2 . side c is known as the hypotenuse. the hypotenuse is the longest side of. How to use the pythagorean theorem? the pythagorean theorem can be used when we know the length of two sides of a right triangle and we need to get the length of the third side. example 1: find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 3 inches and 4 inches. solution: step 1: write down the formula. In right a triangle, the square of longest side known as the hypotenuse is equal to the sum of the squares of the other two sides. the pythagorean theorem guarantees that if we know the lengths of two sides of a right triangle, we can always determine the length of the third side. our goal is to solve for the length of the hypotenuse. 3. identify a right triangle. for instance, determine whether the triangle is right, given side lengths of 9, 12, and 15 cm. the formula for pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides. [15] the longest side length is the potential hypotenuse.

How To Prove The Pythagorean Theorem 6 Steps With Pictures In right a triangle, the square of longest side known as the hypotenuse is equal to the sum of the squares of the other two sides. the pythagorean theorem guarantees that if we know the lengths of two sides of a right triangle, we can always determine the length of the third side. our goal is to solve for the length of the hypotenuse. 3. identify a right triangle. for instance, determine whether the triangle is right, given side lengths of 9, 12, and 15 cm. the formula for pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides. [15] the longest side length is the potential hypotenuse. In this diagram, it's the missing side x. c = x. step 2: plug the values into the pythagorean theorem. step 3: simplify. square each part and rewrite the equation. step 4: solve for the missing value. the 36 and the 49 are on the same side of the equals sign, so we can add them together and rewrite it as an 85. So we know that the sum of the squares of the other side is going to be equal to c squared. so by the pythagorean theorem, 9 squared plus 7 squared is going to be equal to c squared. 9 squared is 81, plus 7 squared is 49. 80 plus 40 is 120. then we're going to have the 1 plus the 9, that's another 10, so this is going to be equal to 130.
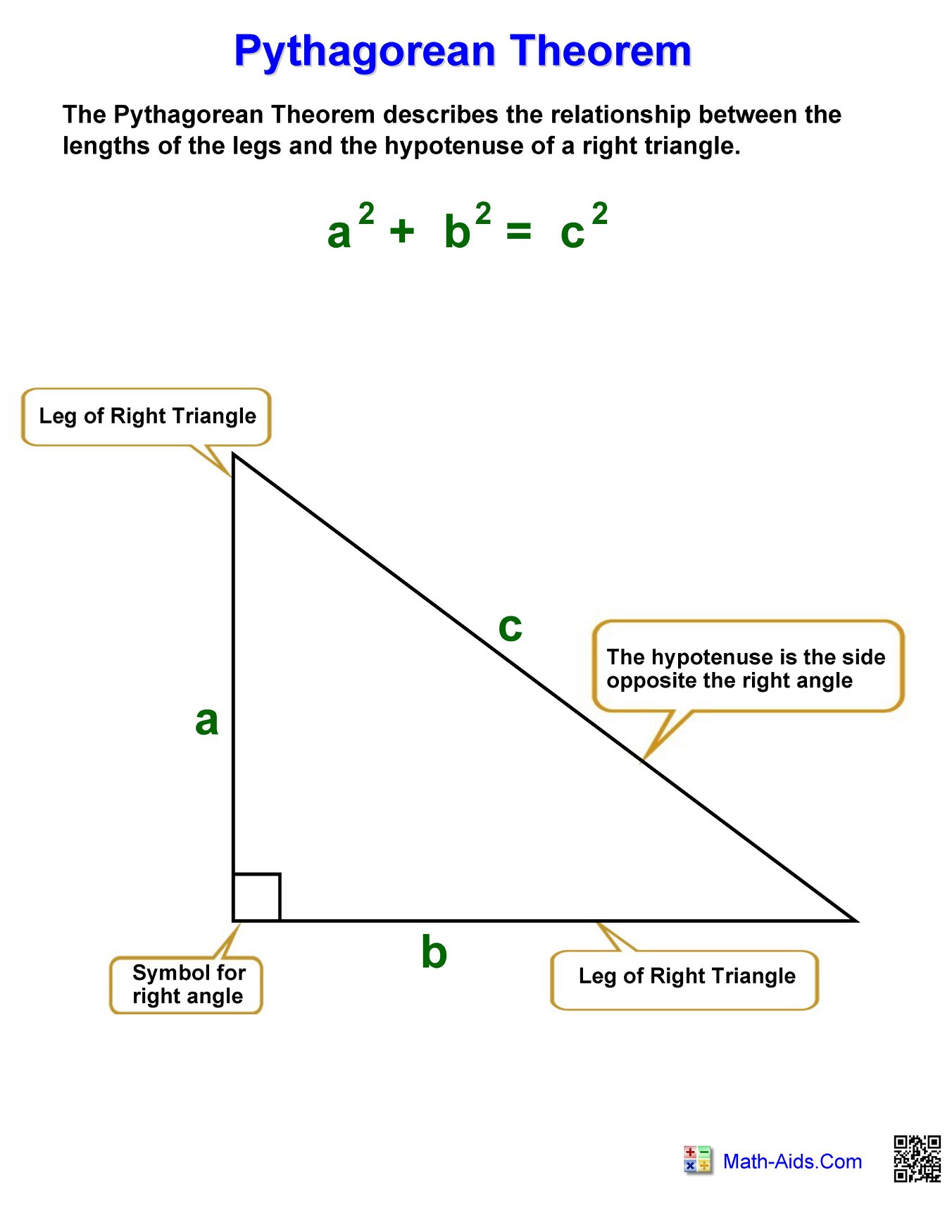
Pythagorean Theorem Chart Hoeden At Home In this diagram, it's the missing side x. c = x. step 2: plug the values into the pythagorean theorem. step 3: simplify. square each part and rewrite the equation. step 4: solve for the missing value. the 36 and the 49 are on the same side of the equals sign, so we can add them together and rewrite it as an 85. So we know that the sum of the squares of the other side is going to be equal to c squared. so by the pythagorean theorem, 9 squared plus 7 squared is going to be equal to c squared. 9 squared is 81, plus 7 squared is 49. 80 plus 40 is 120. then we're going to have the 1 plus the 9, that's another 10, so this is going to be equal to 130.

Comments are closed.