Les Nombres Entiers Premiere Partie Un Peu De Mathematiques

Les Nombres Entiers Première Partie Un Peu De Mathématiques Règle. pour pouvoir lire les grands nombres entiers facilement, on regroupe les chiffres par tranches de trois en partant de la droite. exemple : 1049658723 s’écrit 1 049 658 723. on peut utiliser un tableau comme celui ci : ce nombre s’écrit : un milliard quarante neuf millions six cent cinquante huit mille sept cent vingt trois. Le chapitre i sur la partie arithmétique est ici. le chapitre ii sur les nombres complexes est ici. date contenu du cours travail à faire pour 2 9 chapitre i arithmétique partie : divisibilité et congruences dans $\mathbb z$ i relation de divisibilité dans z 0.

Les Nombres Entiers Tu peux aussi te rendre sur socrative dans la salle "pratiquecalcul" pour pratiquer les opérations sur les nombres entiers (4 opérations). plan d'étude pour l'examen du chapitre 1 1re partie 05chapitre 1 plan etude 1repartie.docx. 2 sur 5 yvan monka – académie de strasbourg – maths et tiques.fr 2. nombres rationnels définition : un nombre rationnel est une fraction (*). l'ensemble des nombres rationnels est noté ℚ. Les nombres 1 521, 46 1 521, 46 et − 95,431 − 95,431 ne font pas partie des nombres entiers, car ils possèdent une partie décimale non nulle. il en va de même pour la fraction 20 3 . 20 3 . en utilisant la notation appropriée, on obtient − 92 683 ∈ z − 92 683 ∈ z et 1 521 , 46 ∉ z . 1 521 , 46 ∉ z . Un ensemble qui ne contient pas de nombre s’appelle l’ensemble vide et se note ∅. 7. symbole d’exclusion le signe * exclu le nombre 0 d'un ensemble. par exemple, ℝ* est l'ensemble des nombres réels privé de 0. 8. inclusions tous les nombres de l’ensemble des entiers naturels ℕ appartiennent à l’ensemble des entiers relatifs ℤ.
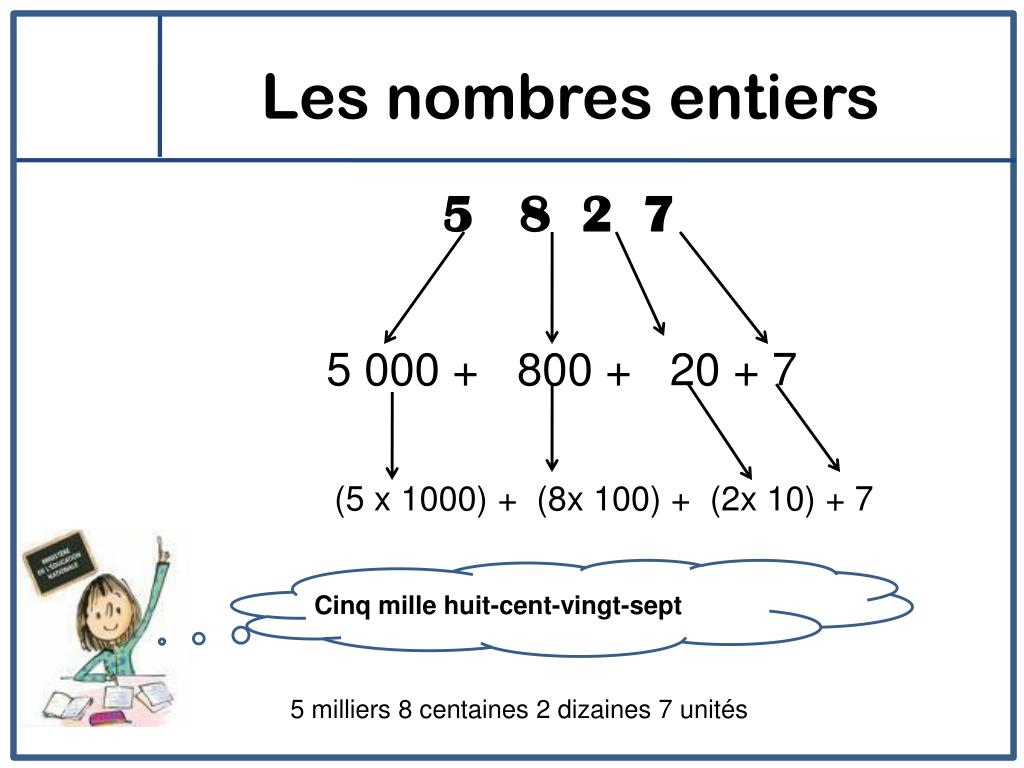
Les Nombres Entiers Les nombres 1 521, 46 1 521, 46 et − 95,431 − 95,431 ne font pas partie des nombres entiers, car ils possèdent une partie décimale non nulle. il en va de même pour la fraction 20 3 . 20 3 . en utilisant la notation appropriée, on obtient − 92 683 ∈ z − 92 683 ∈ z et 1 521 , 46 ∉ z . 1 521 , 46 ∉ z . Un ensemble qui ne contient pas de nombre s’appelle l’ensemble vide et se note ∅. 7. symbole d’exclusion le signe * exclu le nombre 0 d'un ensemble. par exemple, ℝ* est l'ensemble des nombres réels privé de 0. 8. inclusions tous les nombres de l’ensemble des entiers naturels ℕ appartiennent à l’ensemble des entiers relatifs ℤ. Méthode: pour comparer deux nombres entiers, on compte le nombre de chiffres : si les deux nombres ont un nombre de chiffres différent. le nombre le plus grand est celui qui a le plus de chiffres. si les deux nombres ont autant de chiffres. il faut comparer les chiffres les uns après les autres en commençant par la gauche. Nombres entiers. 1. addition de nombres entiers. 2. soustraction de nombres entiers nombres opposés. 4. distance entre 2 points. 5. valeur d’un point sur une.
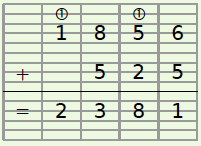
Les Nombres Entiers Première Partie Un Peu De Mathématiques Méthode: pour comparer deux nombres entiers, on compte le nombre de chiffres : si les deux nombres ont un nombre de chiffres différent. le nombre le plus grand est celui qui a le plus de chiffres. si les deux nombres ont autant de chiffres. il faut comparer les chiffres les uns après les autres en commençant par la gauche. Nombres entiers. 1. addition de nombres entiers. 2. soustraction de nombres entiers nombres opposés. 4. distance entre 2 points. 5. valeur d’un point sur une.

Les Nombres Entiers

Comments are closed.