Lecture 5 Stellar Distances
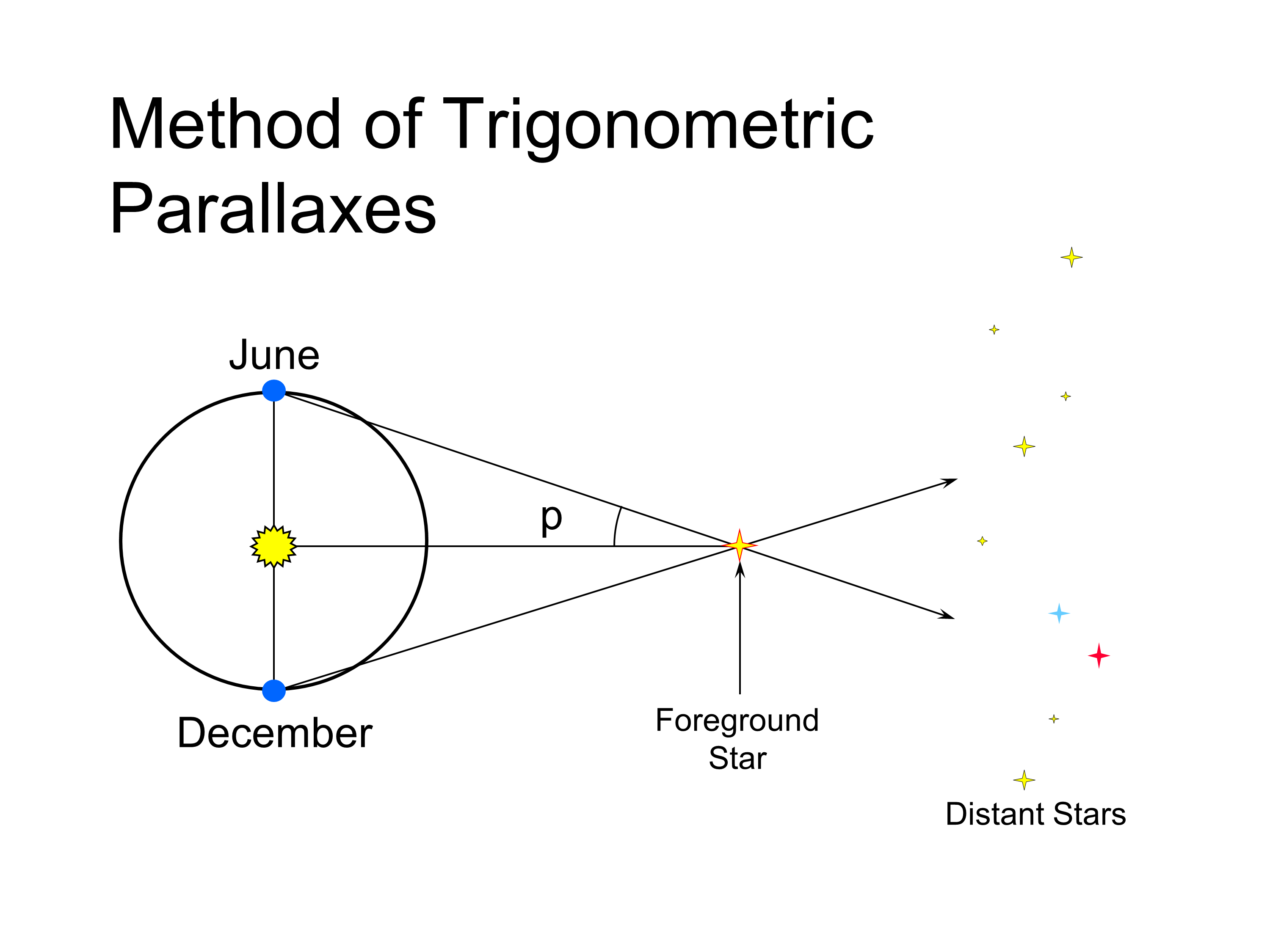
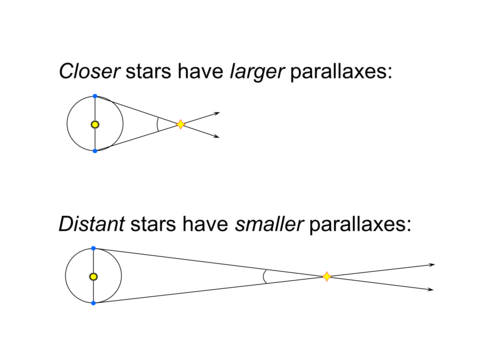
Lecture 5 Stellar Distances Parallax decreases with distance as the distance to a star increases, the its parallax decreases. this is easy to see in the following two figures: (click on the image to view at full scale [size: 165kb]) in the upper figure, the star is about 2.5 times nearer than the star in the lower figure, and has a parallax angle which is 2.5 times larger. Lecture 5: distances of the stars readings: ch 19, section 19 1 key ideas distance is the most important & most difficult quantity to measure in astronomy method of trigonometric parallaxes direct geometric method of finding distances units of cosmic distance: light year parsec (parallax second).

Lecture 5 Stellar Distances Stellar Lecture Parallax Photometric distance determination. in lecture 2, showed that from the definition of absolute magnitude, m, the distance of an object could be calculated if its absolute magnitude is known and its apparent magnitude measured. d = 10 (m m 5) 5 pc. distances determined thus are termed “photometric distances” and the use of standard candles. Parallax decreases with distance as the distance to a star increases, the its parallax decreases. this is easy to see in the following two figures: (graphic by r. pogge) in the upper figure, the star is about 2.5 times nearer than the star in the lower figure, and has a parallax angle which is 2.5 times larger. Images courtesy mike reynolds, ph.d. of florida state college at jacksonville. this diagram (not to scale) shows earth’s orbit about the sun. recall that one orbit is 1 year, 12 months, or 365.24 days. earth is shown twice, at the 12 o’clock position, or e1 , and at the 6 o’clock position, or e2 . these two positions are six months apart. The nearby star is the one that moves and the closer it is the more it moves. s d p! au = d p. s = r p if and only if p is measured in radians! but astronomers actually report the angle p in seconds of arc. radian is 360o 2 = 57.296 and each degree is 3600 arc seconds. so 1 radian = 206265 arc seconds.
Lecture 5 Stellar Distances Images courtesy mike reynolds, ph.d. of florida state college at jacksonville. this diagram (not to scale) shows earth’s orbit about the sun. recall that one orbit is 1 year, 12 months, or 365.24 days. earth is shown twice, at the 12 o’clock position, or e1 , and at the 6 o’clock position, or e2 . these two positions are six months apart. The nearby star is the one that moves and the closer it is the more it moves. s d p! au = d p. s = r p if and only if p is measured in radians! but astronomers actually report the angle p in seconds of arc. radian is 360o 2 = 57.296 and each degree is 3600 arc seconds. so 1 radian = 206265 arc seconds. As earth and observer orbits the sun, the specific star being observed will appear to move relative to the background stars. parallax is the only method for directly measuring stellar distances. you may try this by holding a finger up at arm’s length. open one eye and close the other. now blink; reverse the open closed eyes. L = 4πr2σt4. (stefan’s law) here σ is stefan’s constant and 4πr2 is the surface area of a spherical star of radius r. if we know the luminosity, l, and the temperature t, of a star we can determine its radius r. some stars of a given spectral type are much more luminous (hence larger) than main sequence stars of the same type.

Comments are closed.