Least Squares Cuemath

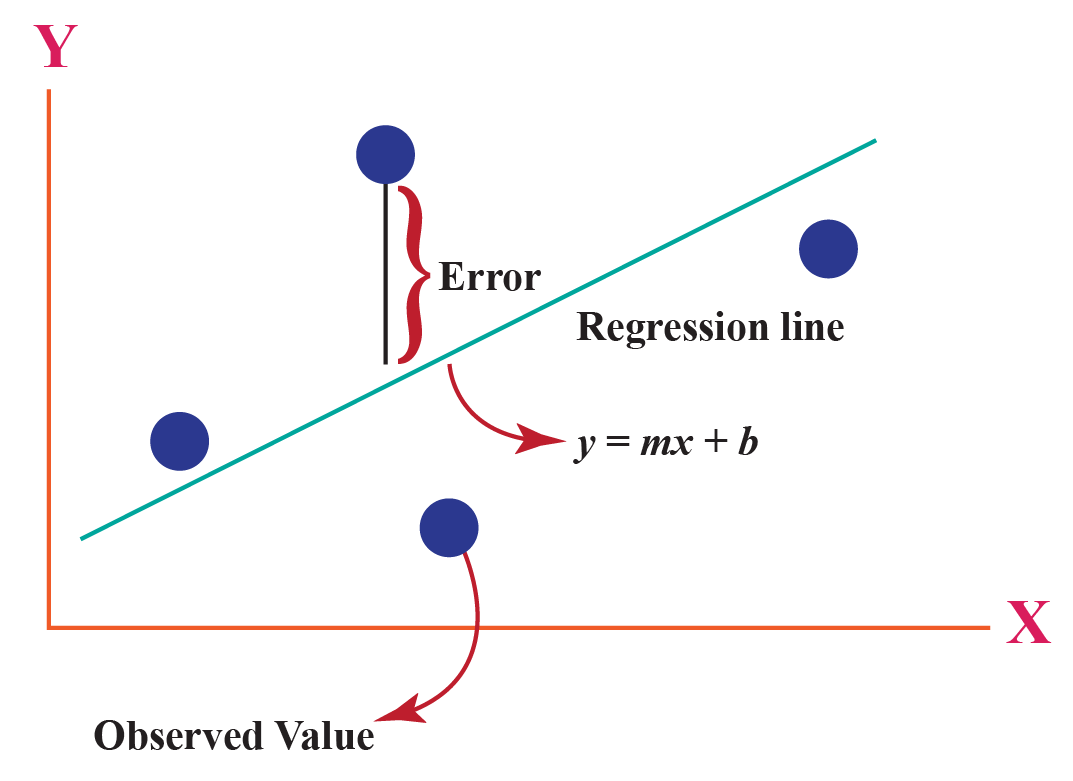
Least Squares Cuemath Following are the steps to calculate the least square using the above formulas. step 1: draw a table with 4 columns where the first two columns are for x and y points. step 2: in the next two columns, find xy and (x) 2. step 3: find ∑x, ∑y, ∑xy, and ∑ (x) 2. step 4: find the value of slope m using the above formula. Step 2 click on "calculate" to find the least square line for the given data. step 3 click on "reset" to clear the fields and enter a new set of values. how to calculate least squares? the least squares method is used to find a linear line of the form y = mx b. here, 'y' and 'x' are variables, 'm' is the slope of the line and 'b' is the y.

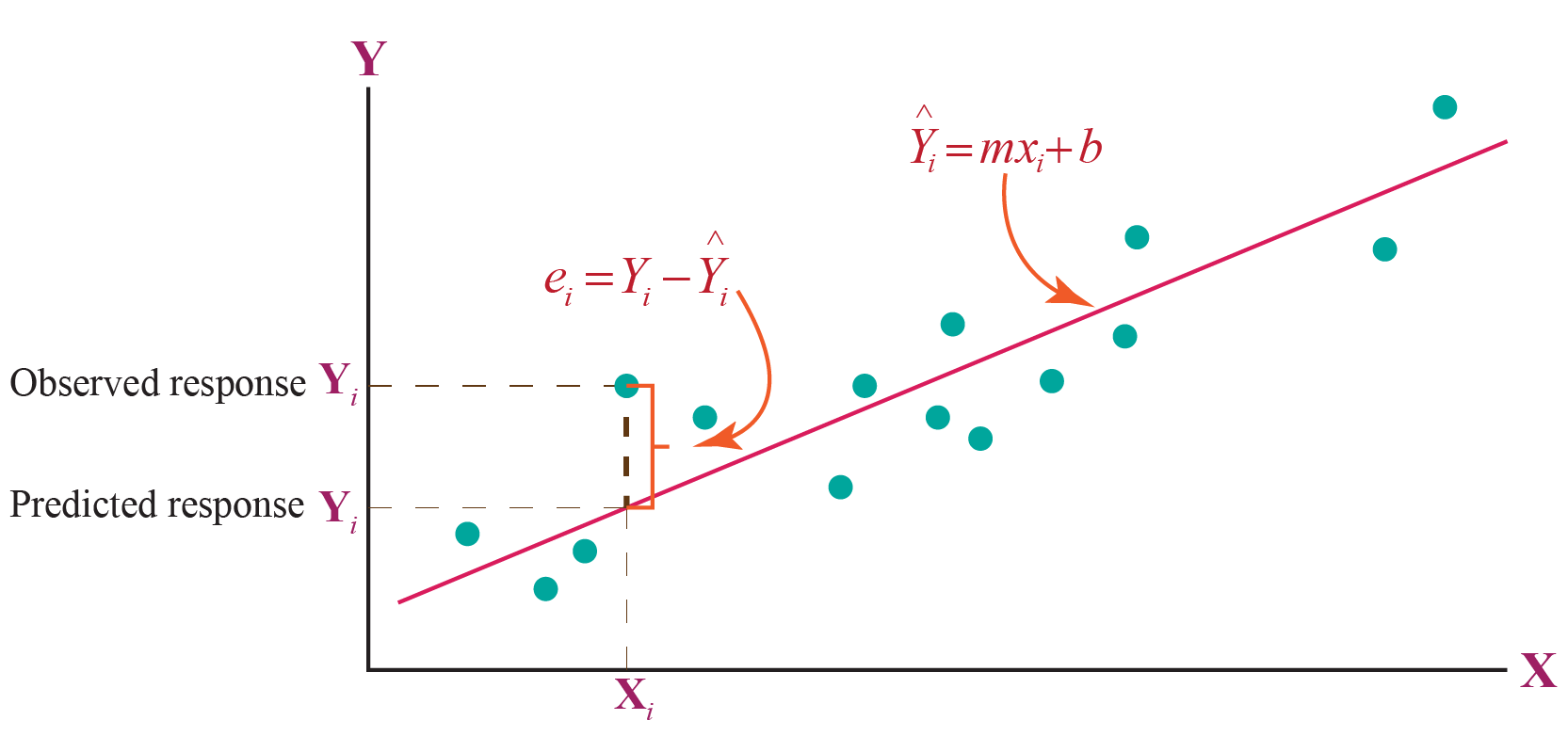
Least Squares Cuemath Explanation: the least squares method is used in statistics to find the line of best fit to the given data. the line is of the form y = mx b. the line so obtained using the least squares method is called the regression line. the main aim of this method is to minimize the sum of the squares of errors as much as possible. A least squares solution of the matrix equation ax = b is a vector k x in r n such that. dist ( b , a k x ) ≤ dist ( b , ax ) for all other vectors x in r n . recall that dist ( v , w )= a v − w a is the distance between the vectors v and w . the term “least squares” comes from the fact that dist ( b , ax )= a b − a k x a is the. The result of fitting a set of data points with a quadratic function conic fitting a set of points using least squares approximation. the method of least squares is a parameter estimation method in regression analysis based on minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the. Recipe 1: compute a least squares solution. let a be an m × n matrix and let b be a vector in rn. here is a method for computing a least squares solution of ax = b: compute the matrix ata and the vector atb. form the augmented matrix for the matrix equation atax = atb, and row reduce.

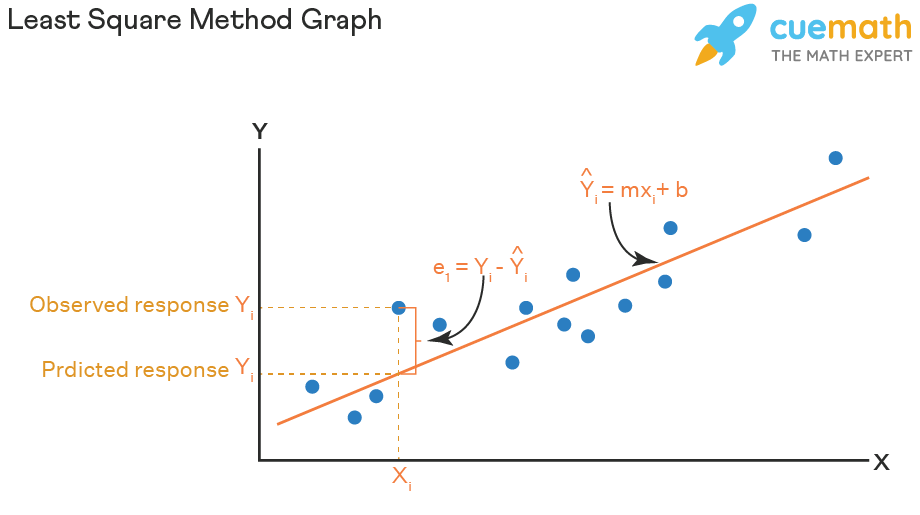
Least Square Method Formula Definition Examples The result of fitting a set of data points with a quadratic function conic fitting a set of points using least squares approximation. the method of least squares is a parameter estimation method in regression analysis based on minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the. Recipe 1: compute a least squares solution. let a be an m × n matrix and let b be a vector in rn. here is a method for computing a least squares solution of ax = b: compute the matrix ata and the vector atb. form the augmented matrix for the matrix equation atax = atb, and row reduce. A least squares regression line represents the relationship between variables in a scatterplot. the procedure fits the line to the data points in a way that minimizes the sum of the squared vertical distances between the line and the points. it is also known as a line of best fit or a trend line. in the example below, we could look at the data. The formula for the line of the best fit with least squares estimation is then: y = a · x b. as you can see, the least square regression line equation is no different from linear dependency's standard expression. the magic lies in the way of working out the parameters a and b. 💡 if you want to find the x intercept, give our slope.

Least Square Method Formula Definition Examples A least squares regression line represents the relationship between variables in a scatterplot. the procedure fits the line to the data points in a way that minimizes the sum of the squared vertical distances between the line and the points. it is also known as a line of best fit or a trend line. in the example below, we could look at the data. The formula for the line of the best fit with least squares estimation is then: y = a · x b. as you can see, the least square regression line equation is no different from linear dependency's standard expression. the magic lies in the way of working out the parameters a and b. 💡 if you want to find the x intercept, give our slope.