Learn To Find Corresponding Angles From A Figure

Learn To Find Corresponding Angles From A Figure Youtube 👉 learn how to identify angles from a figure. this video explains how to solve problems using angle relationships between parallel lines and transversal. we. When two lines are crossed by another line (called the transversal): the angles in matching corners are called corresponding angles. in this example a and e are corresponding angles. also: • b and f are corresponding angles. • c and g are corresponding angles. • d and h are corresponding angles.
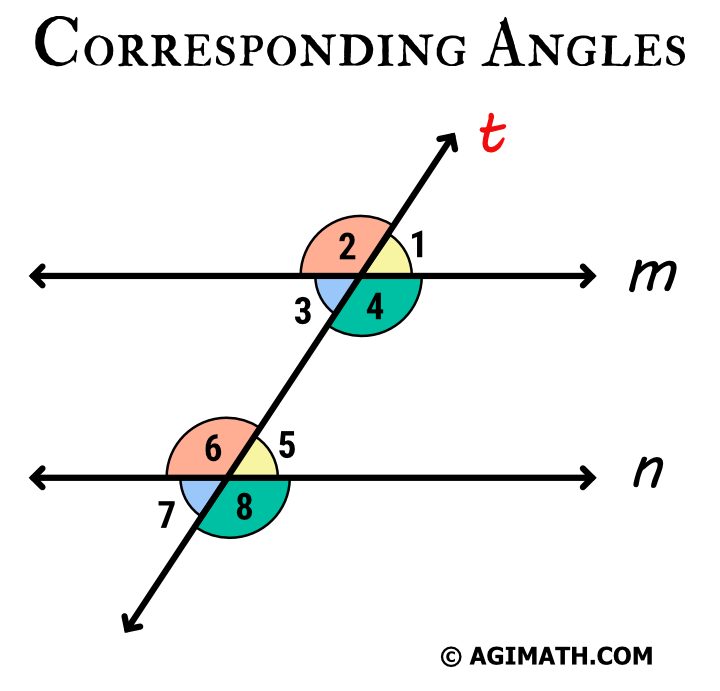
Corresponding Angles Agimath Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles. The other corresponding pairs of angles in the above diagram are: b and f; c and g; a and e. (corresponding angles found in a f shaped figure) example: in the following diagram, all the lines shown are straight lines. line m is parallel to line n. list a pair of corresponding angle. solution: d and h are corresponding angles. Corresponding angles are formed when a transversal intersects two parallel lines. these angles are located on the same side of the transversal in corresponding positions. corresponding angles are always formed in pairs and are congruent. in the figure, we can see that a transversal line is intersecting the parallel lines ‘a’ and ‘b’.
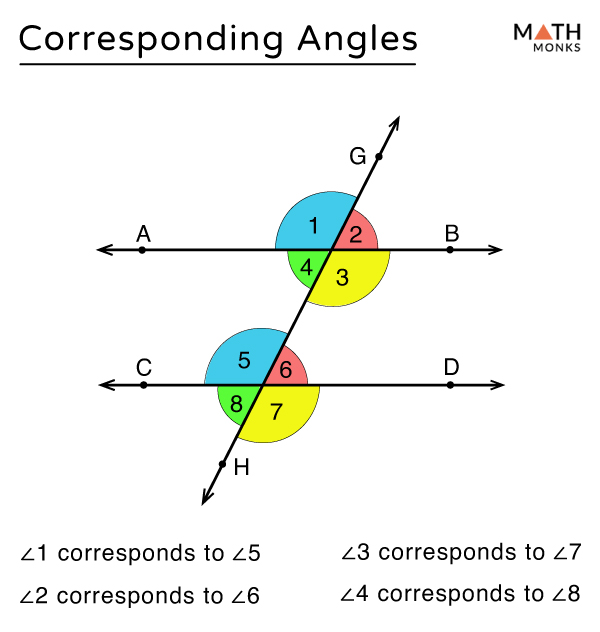
Corresponding Angles Definition Theorem With Examples The other corresponding pairs of angles in the above diagram are: b and f; c and g; a and e. (corresponding angles found in a f shaped figure) example: in the following diagram, all the lines shown are straight lines. line m is parallel to line n. list a pair of corresponding angle. solution: d and h are corresponding angles. Corresponding angles are formed when a transversal intersects two parallel lines. these angles are located on the same side of the transversal in corresponding positions. corresponding angles are always formed in pairs and are congruent. in the figure, we can see that a transversal line is intersecting the parallel lines ‘a’ and ‘b’. Example 1: corresponding angles. calculate the size of the missing angle θ. justify your answer. highlight the angle (s) that you already know. 2 use corresponding angles to find a missing angle. here we can label the corresponding angle on the diagram as 75°. 3 use a basic angle fact to calculate the missing angle. The two corresponding angles are always congruent. hence, 9x 10 = 55. 9x = 55 – 10. 9x = 45. x = 5. example 3. the two corresponding angles of a figure measure 7y – 12 and 5y 6. find the magnitude of a corresponding angle. solution. first, we need to determine the value of y. the two corresponding angles are always congruent. hence, 7y.

How To Determine Corresponding Angles And Sides Identifying Congruent Example 1: corresponding angles. calculate the size of the missing angle θ. justify your answer. highlight the angle (s) that you already know. 2 use corresponding angles to find a missing angle. here we can label the corresponding angle on the diagram as 75°. 3 use a basic angle fact to calculate the missing angle. The two corresponding angles are always congruent. hence, 9x 10 = 55. 9x = 55 – 10. 9x = 45. x = 5. example 3. the two corresponding angles of a figure measure 7y – 12 and 5y 6. find the magnitude of a corresponding angle. solution. first, we need to determine the value of y. the two corresponding angles are always congruent. hence, 7y.

Geometry Identifying Corresponding Angles From A Figure Youtube
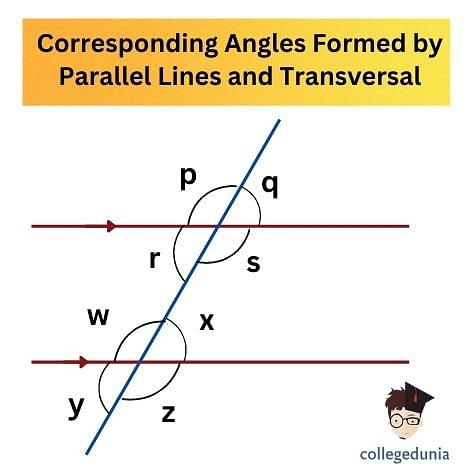
Corresponding Angles Definition Types Theorem Examples

Comments are closed.