Law Of Logarithms With Examples

Logarithm Laws Made Easy A Complete Guide With Examples Mathsathome The product (addition) logarithm law. to add two or more logarithms that have the same base, simply multiply the numbers inside the logarithms. for example, log(3) log(2) = log(6). the result is a single logarithm with the same base as those being added. the formula for the product law of logarithms is given as: the product rule of logarithm laws. The logarithm of the ratio of two quantities is the logarithm of the numerator minus the logarithm of the denominator. the logarithm of an exponential number is the exponent times the logarithm of the base. the logarithm of the argument (inside the parenthesis) wherein the argument equals the base is equal to . for for b> 0 b>0.
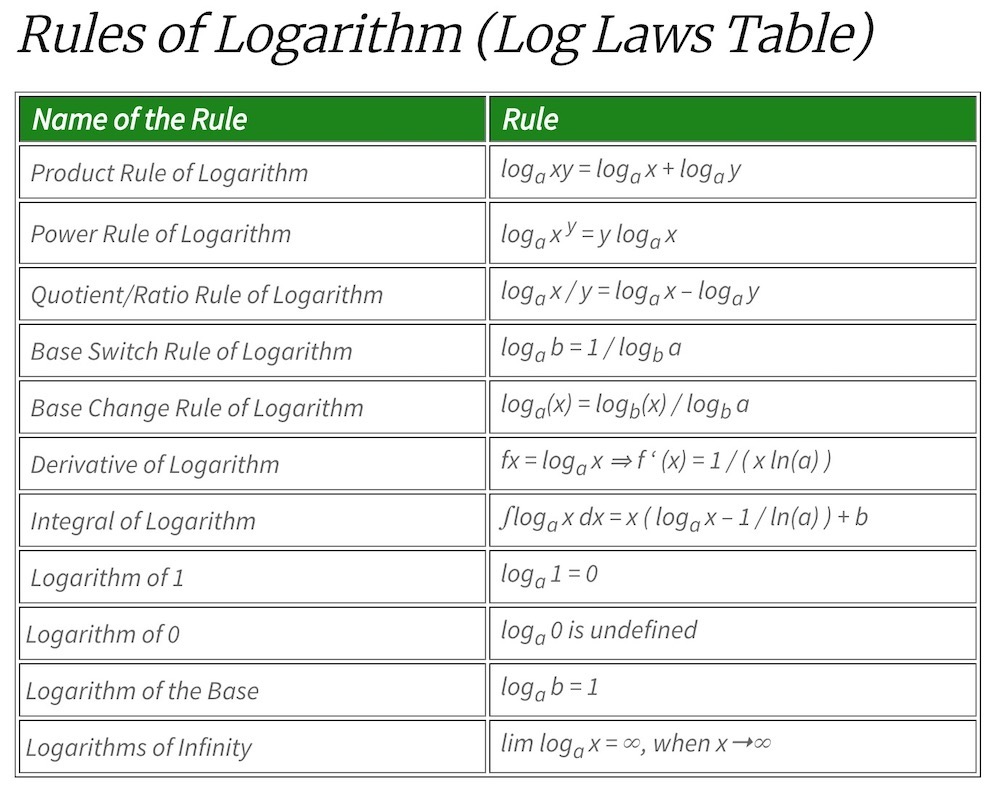
Logarithm Rules Aka Log Laws Explained With Examples Maths For Kids Using laws of logarithms (laws of logs) to solve log problems. the general log rule to convert log functions to exponential functions and vice versa. we know already the general rule that allows us to move back and forth between the logarithm and exponents. and we can continue to use this rule whenever it makes sense in any of these log problems. The four basic laws of logarithms include: the product rule law. the first law of logarithms state that the sum of two logarithms is equal to the product of the logarithms. the first law is represented as; log a log b = log ab. example: log 2 5 log 2 4 = log 2 (5 × 4) = log 2 20; log 10 6 log 10 3 = log 10 (6 x 3) = log 10 18. Notice that we used the product rule for logarithms to find a solution for the example above. by doing so, we have derived the power rule for logarithms, which says that the log of a power is equal to the exponent times the log of the base. keep in mind that, although the input to a logarithm may not be written as a power, we may be able to. Although technically a logarithm law, it is important to remember logarithms can be converted into exponentials: \(\log a(b) = x\) can be written as \(a^x = b\). law of logs proof. it is not necessary to be able to prove each logarithm law for the exam, but it is important to understand each step and why it occurs. product (addition) law.

14 Laws Of Logarithms Ppt Logarithm Algebra Notice that we used the product rule for logarithms to find a solution for the example above. by doing so, we have derived the power rule for logarithms, which says that the log of a power is equal to the exponent times the log of the base. keep in mind that, although the input to a logarithm may not be written as a power, we may be able to. Although technically a logarithm law, it is important to remember logarithms can be converted into exponentials: \(\log a(b) = x\) can be written as \(a^x = b\). law of logs proof. it is not necessary to be able to prove each logarithm law for the exam, but it is important to understand each step and why it occurs. product (addition) law. Logarithms are the inverses of exponents. they allow us to solve challenging exponential equations, and they are a good excuse to dive deeper into the relationship between a function and its inverse. The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator. log a = log a x – log a y. 3) power rule. log a x n = nlog a x. 4) change of base rule. where x and y are positive, and a > 0, a ≠ 1. example: simplify the following, expressing each as a single logarithm: a) log 2 4 log 2 5 b) log a 28.
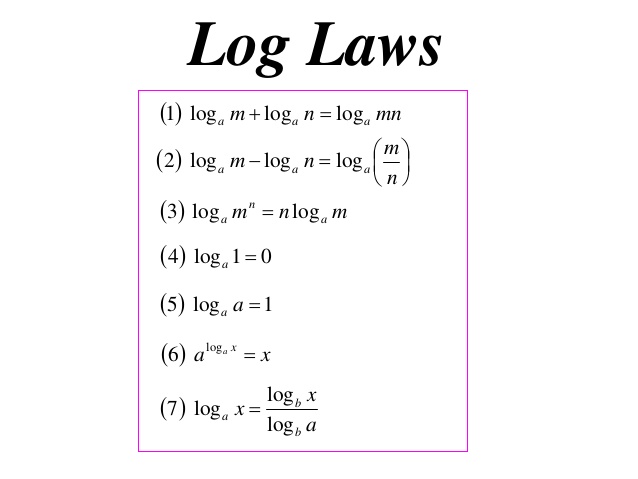
Exercise 7e Logarithms And Laws Of Logarithms Mathematics Tutorial Logarithms are the inverses of exponents. they allow us to solve challenging exponential equations, and they are a good excuse to dive deeper into the relationship between a function and its inverse. The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator. log a = log a x – log a y. 3) power rule. log a x n = nlog a x. 4) change of base rule. where x and y are positive, and a > 0, a ≠ 1. example: simplify the following, expressing each as a single logarithm: a) log 2 4 log 2 5 b) log a 28.

Rules Of Logarithms With Examples

Comments are closed.