Laplace Transform Table Definition Examples In Maths

Laplace Transform Table Definition Examples Maths 4. laplace transforms. 4.1 the definition; 4.2 laplace transforms; 4.3 inverse laplace transforms; 4.4 step functions; 4.5 solving ivp's with laplace transforms; 4.6 nonconstant coefficient ivp's; 4.7 ivp's with step functions; 4.8 dirac delta function; 4.9 convolution integrals; 4.10 table of laplace transforms; 5. systems of de's. 5.1 review. Laplace transform is the integral transform of the given derivative function with real variable t to convert into a complex function with variable s. visit byju’s to learn the definition, properties, inverse laplace transforms and examples.

Laplace Transform Table Definition Examples In Maths We use t as the independent variable for f because in applications the laplace transform is usually applied to functions of time. the laplace transform can be viewed as an operator l that transforms the function f = f(t) into the function f = f(s). thus, equation 7.1.2 can be expressed as. f = l(f). Combining some of these simple laplace transforms with the properties of the laplace transform, as shown in table \(\pageindex{2}\), we can deal with many applications of the laplace transform. we will first prove a few of the given laplace transforms and show how they can be used to obtain new transform pairs. The laplace transform is a mathematical technique that changes a function of time into a function in the frequency domain. if we transform both sides of a differential equation, the resulting equation is often something we can solve with algebraic methods. Laplace transform. in mathematics, the laplace transform, named after pierre simon laplace ( ləˈplɑːs ), is an integral transform that converts a function of a real variable (usually , in the time domain) to a function of a complex variable (in the complex valued frequency domain, also known as s domain, or s plane).
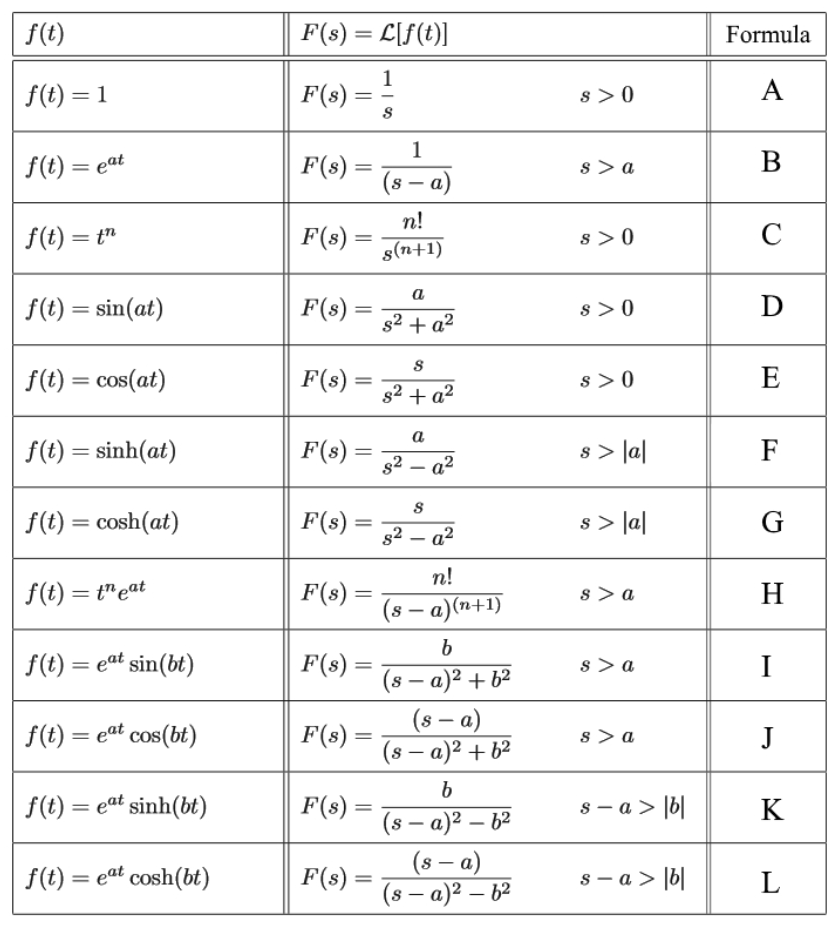
Formula Of Laplace Transform The laplace transform is a mathematical technique that changes a function of time into a function in the frequency domain. if we transform both sides of a differential equation, the resulting equation is often something we can solve with algebraic methods. Laplace transform. in mathematics, the laplace transform, named after pierre simon laplace ( ləˈplɑːs ), is an integral transform that converts a function of a real variable (usually , in the time domain) to a function of a complex variable (in the complex valued frequency domain, also known as s domain, or s plane). The main idea behind the laplace transformation is that we can solve an equation (or system of equations) containing differential and integral terms by transforming the equation in " t space" to one in " s space". this makes the problem much easier to solve. the kinds of problems where the laplace transform is invaluable occur in electronics. A laplace transform is a method used to solve ordinary differential equations (odes). it is an integral transformation that transforms a continuous piecewise function into a simpler form that allows us to solve complicated differential equations using algebra. recall that a piecewise continuous function is a function that has a finite number of.

Laplace Transform Table Definition Examples In Maths The main idea behind the laplace transformation is that we can solve an equation (or system of equations) containing differential and integral terms by transforming the equation in " t space" to one in " s space". this makes the problem much easier to solve. the kinds of problems where the laplace transform is invaluable occur in electronics. A laplace transform is a method used to solve ordinary differential equations (odes). it is an integral transformation that transforms a continuous piecewise function into a simpler form that allows us to solve complicated differential equations using algebra. recall that a piecewise continuous function is a function that has a finite number of.

Comments are closed.