La Circunferencia Y Sus Partes Carpeta Aprende Con Serlo

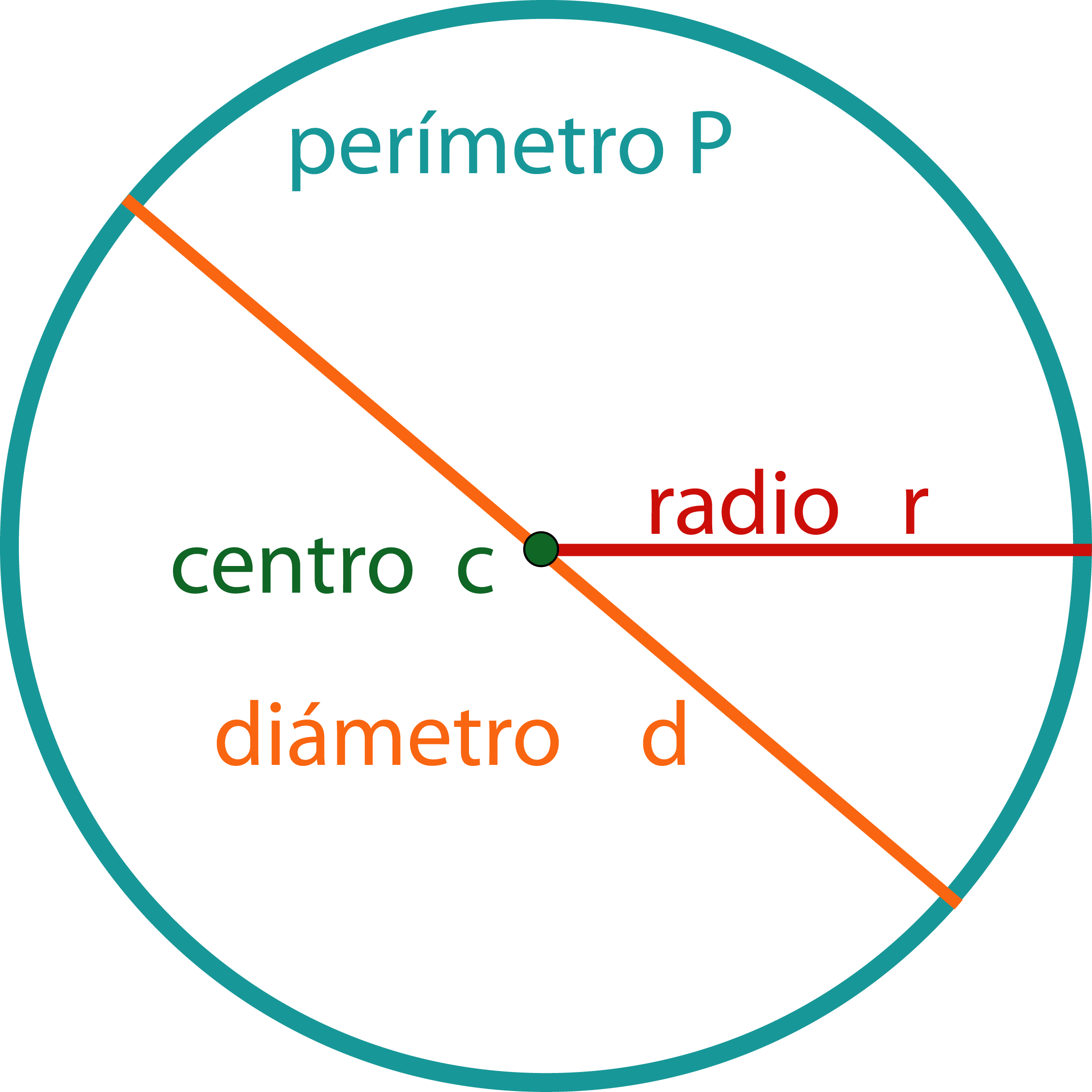
La Circunferencia Y Sus Partes Carpeta Aprende Con Serlo Perímetro. la longitud de la línea que forma la circunferencia se llama perímetro. la relación entre la circunferencia y el diámetro es el número π del círculo. este representa al numero π multiplicado por el diámetro: p=π \cdot d p = π ⋅ d. . longitud de la ciurcunferencia. La circunferencia y sus partes – fundamentos y ejercicios. contenido pie de página. la plataforma para el aprendizaje abierto. temas. sobre serlo. ¡participa! comunidad. root matemáticas geometría triángulos, cuadriláteros, círcunferencias y otras figuras planas.

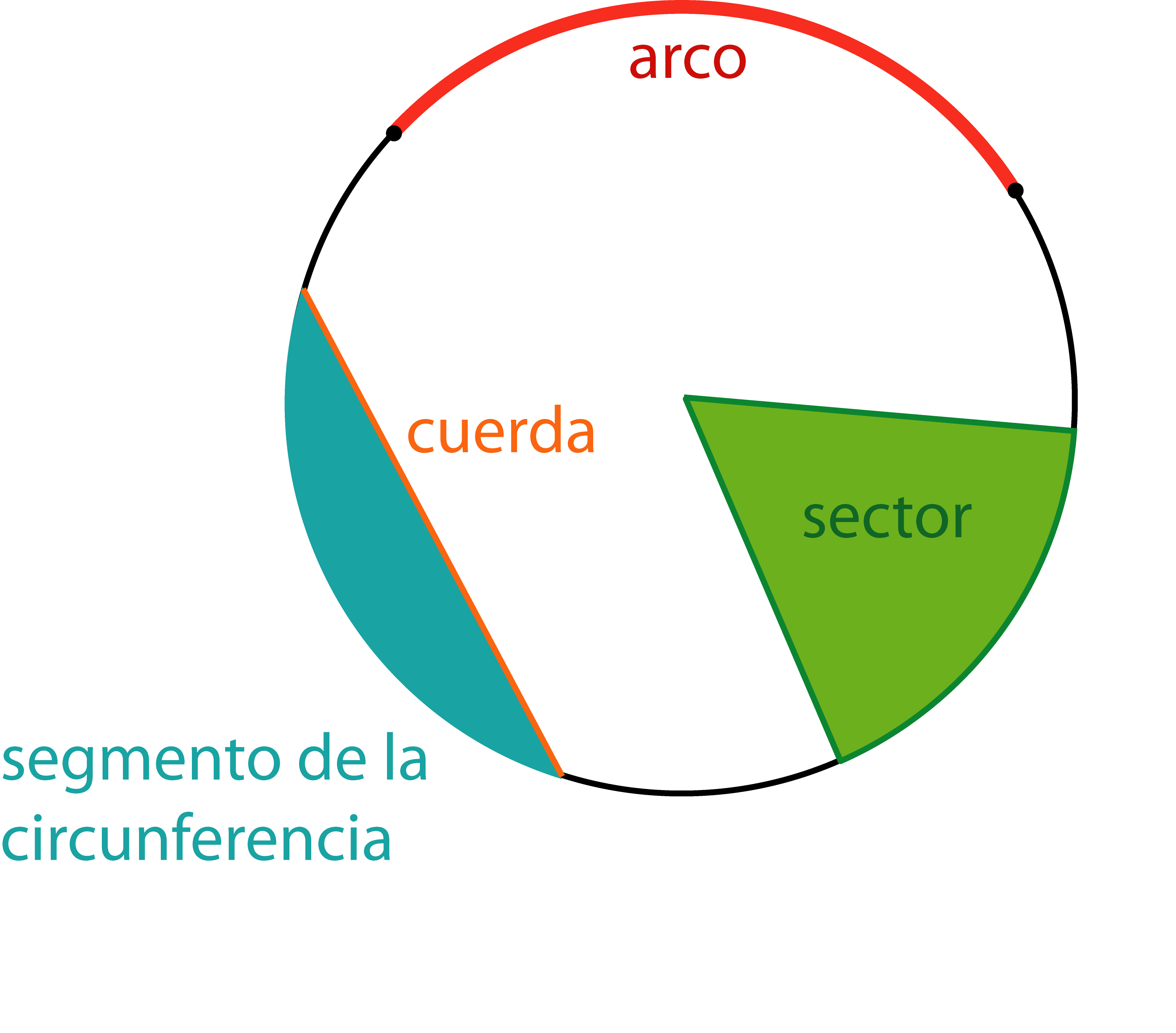
Circunferencia Aprende Con Serlo Aproximadamente es \mathrm\pi\approx3,14159 . \pi es la relación entre la circunferencia de un círculo y su diámetro. se cumple: \pi = \dfrac{\color{#009999}u}{\color{#cc0000}d} . importante: para asegurarte de que todas las imágenes y fórmulas se impriman, por favor desplázate hacia abajo hasta el final de la página una vez antes de. Las partes de la circunferencia son conceptos fundamentales en el estudio de la geometría, un área que nos permite comprender mejor las formas y figuras que nos rodean. . la circunferencia es una de las figuras más importantes en estas matemáticas, ya que es un ejemplo clásico de una figura bidimensional cuyas propiedades son ampliamente utilizadas en diversas aplicaciones práctic. 2 diagrama de una circunferencia. 2.1 el centro: punto de referencia. 2.2 el radio: conexión entre el centro y la circunferencia. 2.3 el arco: porciones de la circunferencia. 2.4 la cuerda: uniendo dos puntos. 2.5 el diámetro: la cuerda más larga. 2.6 la tangente: tocando sin cruzar. En este caso, el perímetro es la longitud de la circunferencia → p = 2 π r; y la apotema es igual al radio a = r. sustituyendo estos valores en la fórmula → a = (2 π r x r) 2 = π r2 nos queda: a = π r2. fórmula que nos permite calcular el Área de cualquier círculo conociendo su radio.

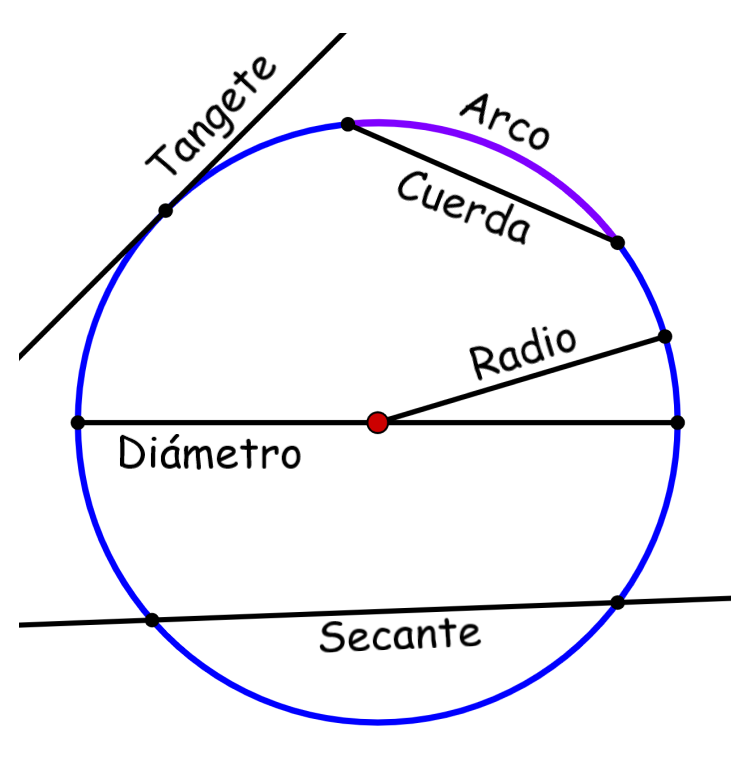
Partes De Una Circunferencia Con Diagramas Neurochispas 2 diagrama de una circunferencia. 2.1 el centro: punto de referencia. 2.2 el radio: conexión entre el centro y la circunferencia. 2.3 el arco: porciones de la circunferencia. 2.4 la cuerda: uniendo dos puntos. 2.5 el diámetro: la cuerda más larga. 2.6 la tangente: tocando sin cruzar. En este caso, el perímetro es la longitud de la circunferencia → p = 2 π r; y la apotema es igual al radio a = r. sustituyendo estos valores en la fórmula → a = (2 π r x r) 2 = π r2 nos queda: a = π r2. fórmula que nos permite calcular el Área de cualquier círculo conociendo su radio. Level: 3º, 4º y 5º de primaria. language: spanish (es) id: 282275. 22 06 2020. country code: es. country: spain. school subject: matemáticas (1061956) main content: la circunferencia y sus partes (1123550) from worksheet author:. Si pudiéramos desdoblar la circunferencia y estirarla en línea recta, obtendríamos un segmento cuya longitud es igual a la medida de la circunferencia. esta medida se representa con la letra “c” y se calcula mediante la siguiente fórmula: c = 2πr donde π (pi) es una constante matemática aproximadamente igual a 3,14159.