Key Skill Find The Equation Of A Tangent To A Circle

Key Skill Find The Equation Of A Tangent To A Circle Youtube "find the equation of a tangent to a circle.". Tangent is a line and to write the equation of a line we need two things: 1. slope (m) 2. a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1.
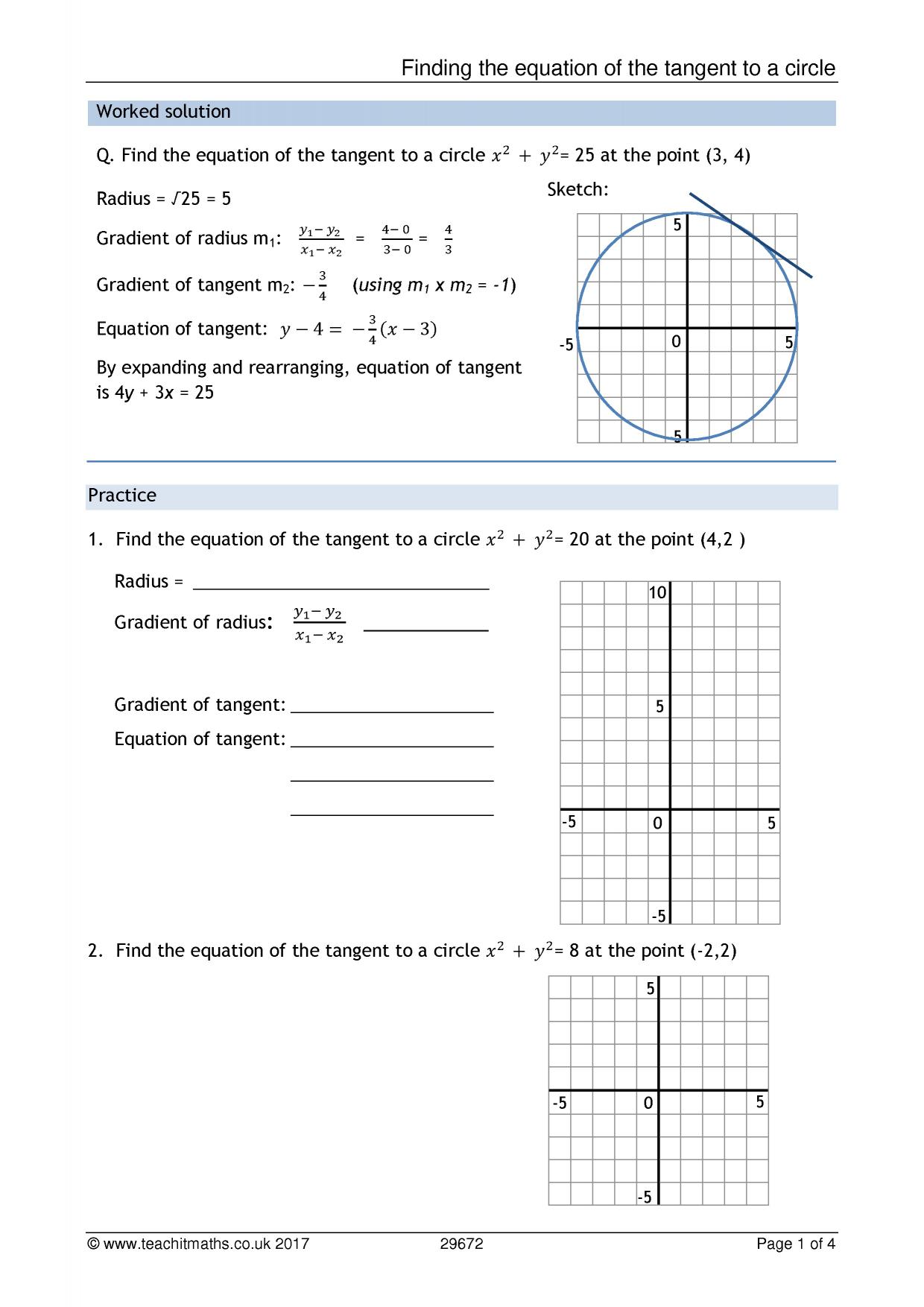
Equation Of A Tangent To A Circle Ks4 Maths Teachit Note: the tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide. also, read: circles; tangent; equation of tangent and normal; general equation. here, the list of the tangent to the circle equation is given below: the tangent to a circle equation x 2 y 2 =a 2 at (x 1, y 1) is xx 1 yy 1. The tangent will have an equation in the form \(y = mx c\) so to find the equation you need to find the values of \(m\) and \(c\). first, find \(m\), the gradient of the tangent. In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. A c = 15 inches and b c = 25 inches. as we know, the radius and tangent of a circle are perpendicular to each other. in abc, applying pythagoras’ theorem. a c 2 a b 2 = b c 2. 15 2 a b 2 = 25 2. a b 2 = 25 2 − 15 2. a b 2 = 25 2 − 15 2. a b 2 = 400. ∴ a b = 20 inches.
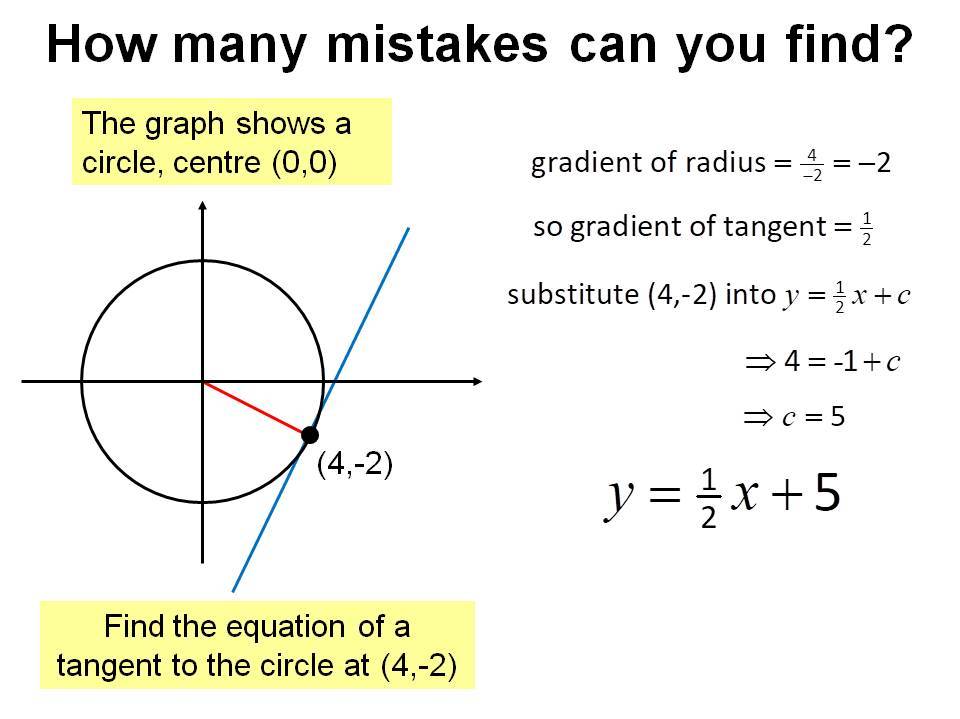
Equation Of Tangent To A Circle Worksheet In the given figure, there is one tangent and one secant. given that, pq = 5 cm, qr = 15 cm. therefore, pr = pq qr = (5 15) = 20 cm. now, according to the formula of the tangent of a circle, sr 2 = pr × qr. sr 2 = 20× 15 = 300 = 17.32 cm. find the length of the tangent pr if the radius of the given circle is 6 m. A c = 15 inches and b c = 25 inches. as we know, the radius and tangent of a circle are perpendicular to each other. in abc, applying pythagoras’ theorem. a c 2 a b 2 = b c 2. 15 2 a b 2 = 25 2. a b 2 = 25 2 − 15 2. a b 2 = 25 2 − 15 2. a b 2 = 400. ∴ a b = 20 inches. Example 1: finding the equation of a tangent. find the equation of the tangent to the circle x^{2} y^{2}=90 at the point (9,3). find the gradient of the radius at that point. the radius is the line joining the centre of the circle (0,0) and the known point on the circumference (9,3). Suppose our circle has center (0;0) and radius 2, and we are interested in tangent lines to the circle that pass through (5;3). the picture we might draw of this situation looks like this. (5;3) we are interested in finding the equations of these tangent lines (i.e., the lines which pass through exactly one point of the circle, and pass.

A16b Finding The Equation Of A Tangent To A Circle At A Given Point Example 1: finding the equation of a tangent. find the equation of the tangent to the circle x^{2} y^{2}=90 at the point (9,3). find the gradient of the radius at that point. the radius is the line joining the centre of the circle (0,0) and the known point on the circumference (9,3). Suppose our circle has center (0;0) and radius 2, and we are interested in tangent lines to the circle that pass through (5;3). the picture we might draw of this situation looks like this. (5;3) we are interested in finding the equations of these tangent lines (i.e., the lines which pass through exactly one point of the circle, and pass.
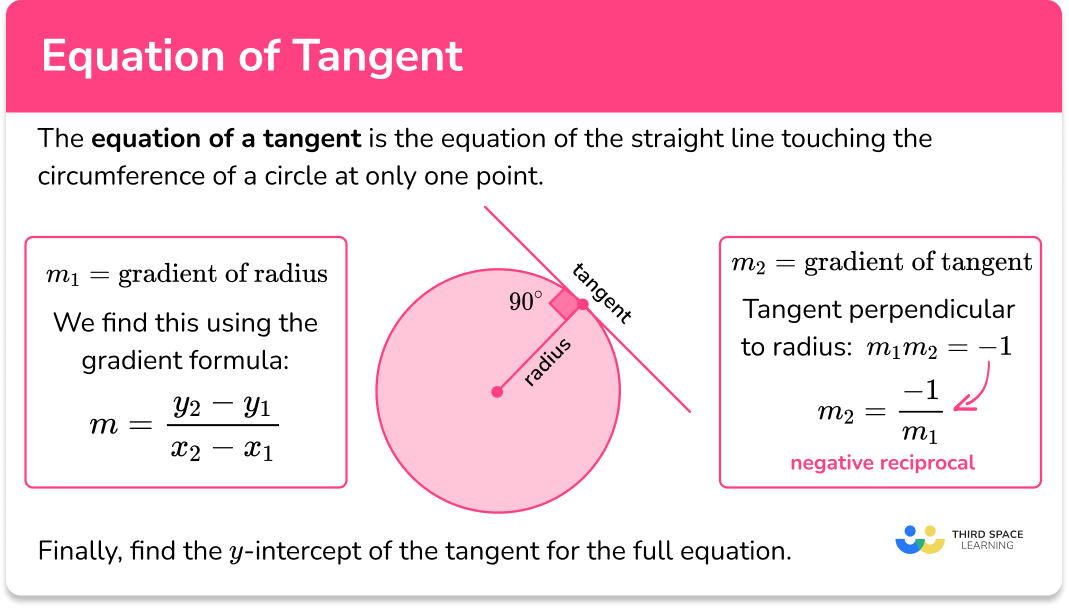
Equation Of Tangent Gcse Maths Steps Examples Worksheet

Comments are closed.