Isometria Y Transformaciones Isometricas

Isometría Y Transformaciones Isométricas Resumen Completo Con Ejemplos Las transformaciones isométricas son cambios de posición u orientación de una determinada figura que no alteran ni la forma ni el tamaño de esta. estas transformaciones son clasificadas en tres tipos: traslación, rotación y reflexión (isometría). en general, las transformaciones geométricas permiten crear una nueva figura a partir de. Transformaciones isométricas por traslación. en una transformación isométrica por traslación se realiza un cambio de posición de la figura en el plano. es un cambio de lugar, determinado por un vector . traslación del punto d a su imagen d’ (vector a = dd’) y traslación de un triángulo. en general, se llama traslación de vector (v.

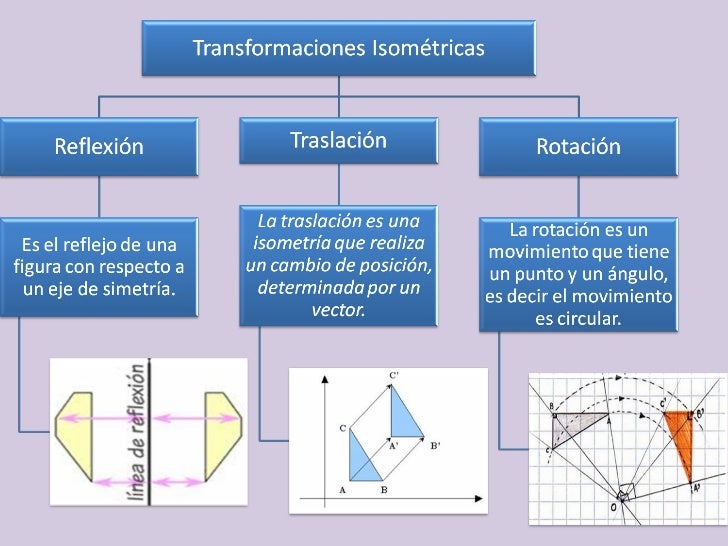
Isometría Y Transformaciones Isométricas Sistema De Coordenadas Pdf Profesor danny perich c. sectormatematica.clmás geometría (2020)Ángulos parte 1 youtu.be r9yxy96z5 uÁngulos parte 2 youtu.be 9pstnpbdzxiÁ. Hay tres tipos principales de transformaciones que entran dentro de la isometría: reflexiones, traslaciones y rotaciones. cualquier transformación que cambie el tamaño o la forma de un objeto no es una isometría, lo que significa quelas dilataciones no son isometrías. una isometría es una transformación realizada sobre un objeto que no. En geometría, una isometría es una transformación que preserva la distancia entre los puntos y los ángulos entre las líneas. en otras palabras, una isometría es una operación en la que la rotación, traslación y reflexión no alteran las longitudes ni las formas de las figuras geométricas. 2 . formalmente si e1 y e2 son dos espacios. Todo esto incluye la transformaciones isométricas. una trasformación isométrica, es modificar de cierta manera algún objeto, el cual no cambia en su forma, pero si en su orientación, dirección o posición en el espacio. estas transformaciones isométricas incluyen la rotación, la traslación y la simetria .

Transformaciones Isométricas Ejercicios Resueltos Ptu Youtube En geometría, una isometría es una transformación que preserva la distancia entre los puntos y los ángulos entre las líneas. en otras palabras, una isometría es una operación en la que la rotación, traslación y reflexión no alteran las longitudes ni las formas de las figuras geométricas. 2 . formalmente si e1 y e2 son dos espacios. Todo esto incluye la transformaciones isométricas. una trasformación isométrica, es modificar de cierta manera algún objeto, el cual no cambia en su forma, pero si en su orientación, dirección o posición en el espacio. estas transformaciones isométricas incluyen la rotación, la traslación y la simetria . 1 transformaciones isométricas. las transformaciones isométricas son cambios de posición (orientación) de una figura determinada que no alteran la forma ni el tamaño de ésta. la palabra isometría tiene origen griego: iso, que significa igual, y metría, que significa medir. por lo tanto, esta palabra puede ser traducida como igual medida. Informalmente, las isometrías en el plano euclidiano son una manera de transformar al plano sin “deformarlo”, manteniendo las distancias. si se piensa en el plano euclidiano como una hoja de plástico transparente sobre una mesa, las distintas isometrías se verían como: desplazar la hoja unos centímetros a la derecha o a la izquierda.
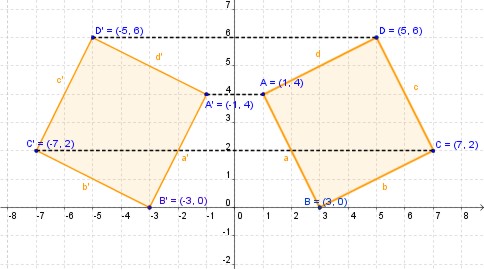
Isometría Y Transformaciones Isométricas 1 transformaciones isométricas. las transformaciones isométricas son cambios de posición (orientación) de una figura determinada que no alteran la forma ni el tamaño de ésta. la palabra isometría tiene origen griego: iso, que significa igual, y metría, que significa medir. por lo tanto, esta palabra puede ser traducida como igual medida. Informalmente, las isometrías en el plano euclidiano son una manera de transformar al plano sin “deformarlo”, manteniendo las distancias. si se piensa en el plano euclidiano como una hoja de plástico transparente sobre una mesa, las distintas isometrías se verían como: desplazar la hoja unos centímetros a la derecha o a la izquierda.

Isometría Y Transformaciones Isométricas Pdf Rotación Simetría
Transformaciones Isometricas I

Comments are closed.