Inverse Laplace Transforms Studypug

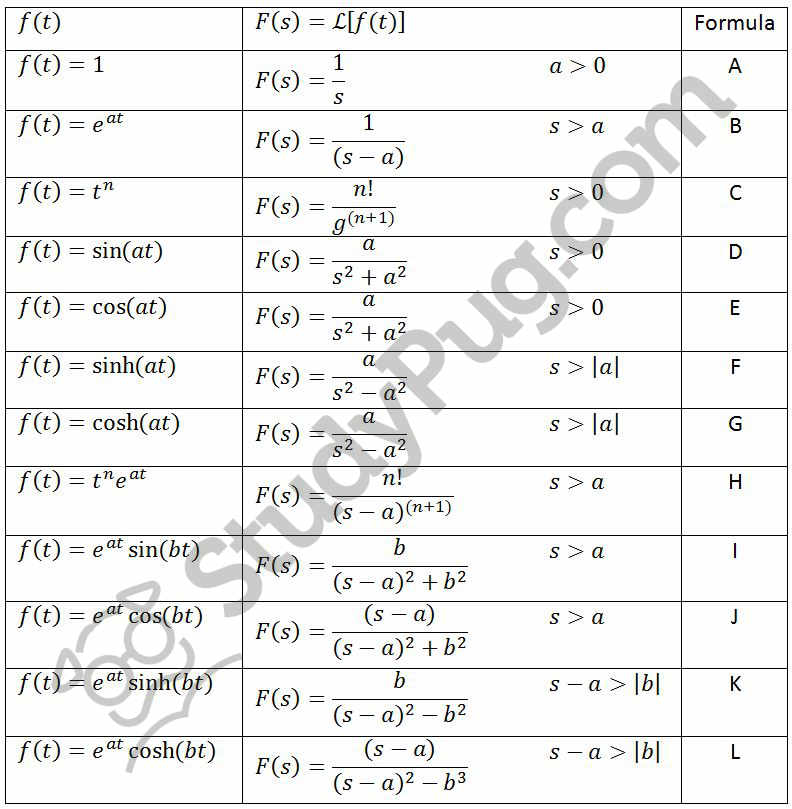
Inverse Laplace Transforms Studypug The inverse laplace transform definition comes as the inverse operation of the laplace transformation and is mathematically is written as: formula 1: inverse laplace transform definition. on its integral form, the inverse laplace transform looks like: formula 2: inverse laplace transform general integral form. Step 2: substitute equation 6 into the equation above to turn all laplace equations into the form l {y}: equation for example 1 (b): substituting the known expressions from equation 6 into the laplace transform. step 3: insert the initial condition values y (0)=2 and y' (0)=6.

Inverse Laplace Transforms Studypug Laplace transform of sine. for this section we have the function f (t)=\sin (wt) f(t)=sin(wt) laplace transform of sine pt.1. let us solve the integral part using integration by parts: laplace transform of sine pt.2. from this notice that the first part of the solution goes to zero: laplace transform of sine pt.3. However, we see from the table of laplace transforms that the inverse transform of the second fraction on the right of equation 8.2.14 will be a linear combination of the inverse transforms. e − tcost and e − tsint. of. s 1 (s 1)2 1 and 1 (s 1)2 1. respectively. therefore, instead of equation 8.2.14 we write. 2. laplace transform definition; 2a. table of laplace transformations; 3. properties of laplace transform; 4. transform of unit step functions; 5. transform of periodic functions; 6. transforms of integrals; 7. inverse of the laplace transform; 8. using inverse laplace to solve des; 9. integro differential equations and systems of des; 10. As you will see this can be a more complicated and lengthy process than taking transforms. in these cases we say that we are finding the inverse laplace transform of f(s) and use the following notation. f(t) = l − 1{f(s)} as with laplace transforms, we’ve got the following fact to help us take the inverse transform.

Solution Inverse Laplace Transforms Studypool 2. laplace transform definition; 2a. table of laplace transformations; 3. properties of laplace transform; 4. transform of unit step functions; 5. transform of periodic functions; 6. transforms of integrals; 7. inverse of the laplace transform; 8. using inverse laplace to solve des; 9. integro differential equations and systems of des; 10. As you will see this can be a more complicated and lengthy process than taking transforms. in these cases we say that we are finding the inverse laplace transform of f(s) and use the following notation. f(t) = l − 1{f(s)} as with laplace transforms, we’ve got the following fact to help us take the inverse transform. The inverse laplace transform is a linear operation. a necessary condition for the existence of the inverse laplace transform is that the function must be absolutely integrable, which means the integral of the absolute value of the function over the whole real axis must converge. in previous posts, we talked about the four types of ode linear. The inverse laplace transform. we can also define the inverse laplace transform: given a function x(s) in the s domain, its inverse laplace transform l−1[x(s)] is a function x(t) such that x(s) = l[x(t)]. it can be shown that the laplace transform of a causal signal is unique; hence, the inverse laplace transform is uniquely defined as well.

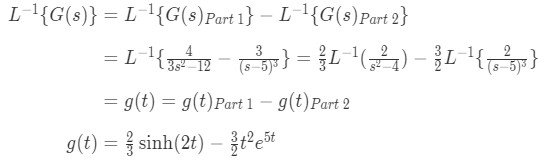
Inverse Laplace Transforms Studypug The inverse laplace transform is a linear operation. a necessary condition for the existence of the inverse laplace transform is that the function must be absolutely integrable, which means the integral of the absolute value of the function over the whole real axis must converge. in previous posts, we talked about the four types of ode linear. The inverse laplace transform. we can also define the inverse laplace transform: given a function x(s) in the s domain, its inverse laplace transform l−1[x(s)] is a function x(t) such that x(s) = l[x(t)]. it can be shown that the laplace transform of a causal signal is unique; hence, the inverse laplace transform is uniquely defined as well.

Solution Inverse Laplace Transforms Studypool

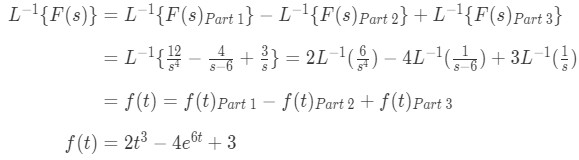
Inverse Laplace Transforms Studypug