Interior Angles Of A Polygon Geometry

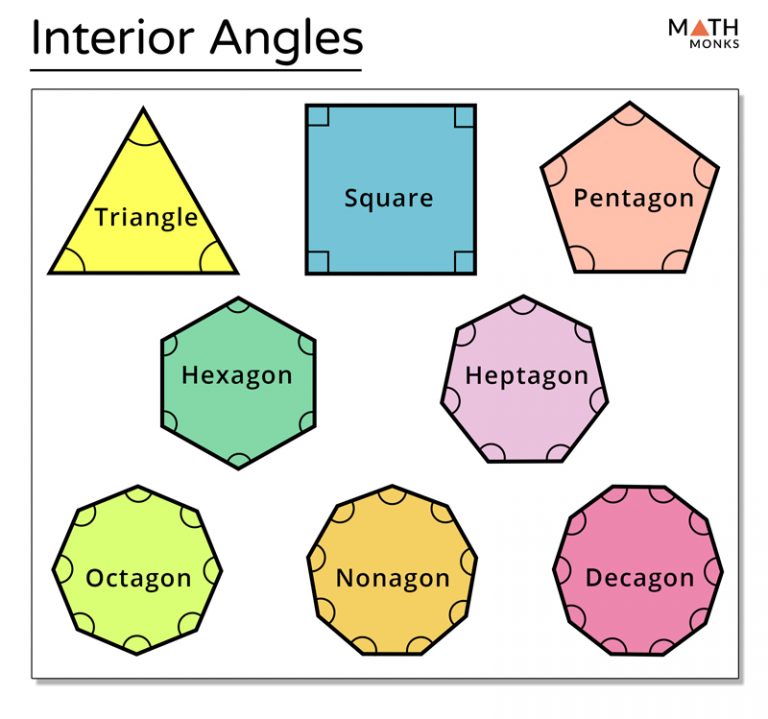
Interior Angles Solved Examples Geometry Cuemath If it is a regular polygon (all sides are equal, all angles are equal) shape sides sum of interior angles shape each angle; triangle: 3: 180° 60° quadrilateral: 4: 360° 90° pentagon: 5: 540° 108° hexagon: 6: 720° 120° heptagon (or septagon) 7: 900° 128.57 ° octagon: 8: 1080° 135° nonagon: 9: 1260° 140° any polygon: n (n−2. What is the sum of the interior angles of a polygon? the sum of the interior angles of a polygon of n sides can be calculated with the formula 180(n 2)°. it helps us in finding the total sum of all the angles of a polygon, whether it is a regular polygon or an irregular polygon. by using this formula, we can verify the angle sum property as.

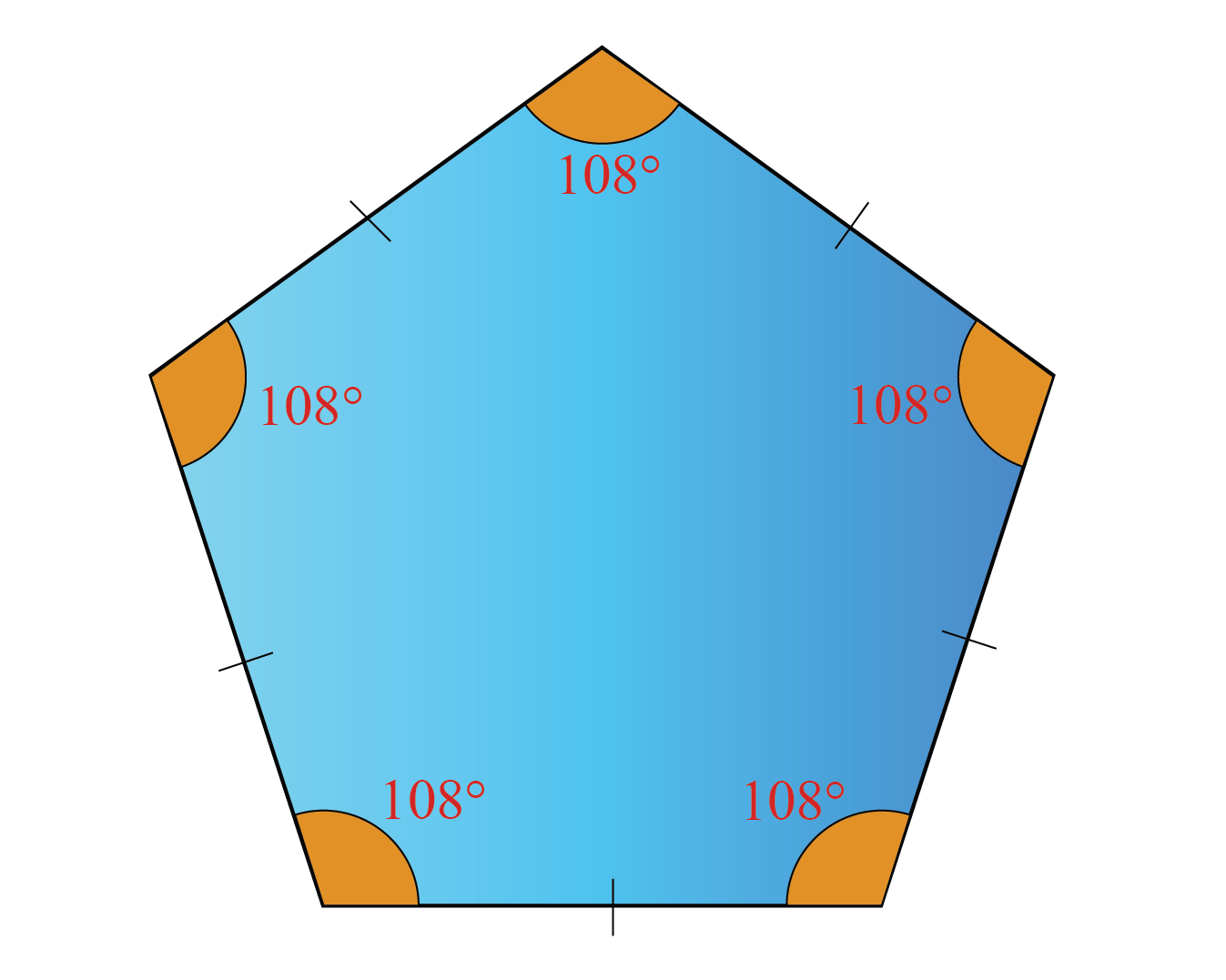
Polygon Geometry Pentagons Hexagons And Dodecagons Interior angles of a polygon. here you will learn about interior angles of a polygon, including how to calculate the sum of interior angles for a polygon, single interior angles, and how to use this knowledge to solve problems. students will first learn about interior angles of a polygon as part of geometry in high school. Let us discuss the three different formulas in detail. method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180° (n) – 360°] n. method 2: if the exterior angle of a polygon is given, then the formula to find the interior angle is. 2 find the sum of interior angles of the polygon(s). sum of interior angles =(n 2)\times{180} as the polygon has 4 sides, n=4, so you can substitute n=4 into the formula. sum of interior angles =(4 2)\times{180}=2\times{180}=360^{\circ} 3 solve the problem using the information gathered. the question is asking for the sum of interior angles of. Since all the interior angles of a regular polygon are equal, each interior angle can be calculated by dividing the sum of the angles by the number of sides. each interior angle of a regular polygon $= \frac{180^\circ \times (n\; \;2)}{n}$ let us use this formula to calculate the interior angle of a regular hexagon.

Interior Angles Of A Polygon Gcse Maths Steps Examples 2 find the sum of interior angles of the polygon(s). sum of interior angles =(n 2)\times{180} as the polygon has 4 sides, n=4, so you can substitute n=4 into the formula. sum of interior angles =(4 2)\times{180}=2\times{180}=360^{\circ} 3 solve the problem using the information gathered. the question is asking for the sum of interior angles of. Since all the interior angles of a regular polygon are equal, each interior angle can be calculated by dividing the sum of the angles by the number of sides. each interior angle of a regular polygon $= \frac{180^\circ \times (n\; \;2)}{n}$ let us use this formula to calculate the interior angle of a regular hexagon. The interior angles of any polygon always add up to a constant value, which depends only on the number of sides. for example the interior angles of a pentagon always add up to 540° no matter if it regular or irregular, convex or concave, or what size and shape it is. the sum of the interior angles of a polygon is given by the formula: sum. =. 180. In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we calculate the sum interior anglesor $$ (\red n 2) \cdot 180 $$ and then divide that sum by the number of sides or $$ \red n$$. the formula.

Interior Angles Of Polygons Mr Mathematics The interior angles of any polygon always add up to a constant value, which depends only on the number of sides. for example the interior angles of a pentagon always add up to 540° no matter if it regular or irregular, convex or concave, or what size and shape it is. the sum of the interior angles of a polygon is given by the formula: sum. =. 180. In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we calculate the sum interior anglesor $$ (\red n 2) \cdot 180 $$ and then divide that sum by the number of sides or $$ \red n$$. the formula.

Interior Angles Of A Polygon Gcse Maths Steps Examples

Interior And Exterior Angles Definitions Formulas With Examples