Interior Angle Sum Property Of Quadrilateral

Angle Sum Property Of A Quadrilateral Examples Maths 1. find the fourth angle of a quadrilateral whose angles are 90°, 45° and 60°. solution: by the angle sum property we know; sum of all the interior angles of a quadrilateral = 360°. let the unknown angle be x. so, 90° 45° 60° x = 360°. 195° x = 360°. x = 360° – 195°. The interior angles of a quadrilateral add up to 360°. this value is calculated from the formula given by the angle sum property of polygons. sum of interior angles = (n − 2) × 180°, where 'n' represents the number of sides of the given polygon. in this case, n = 4.
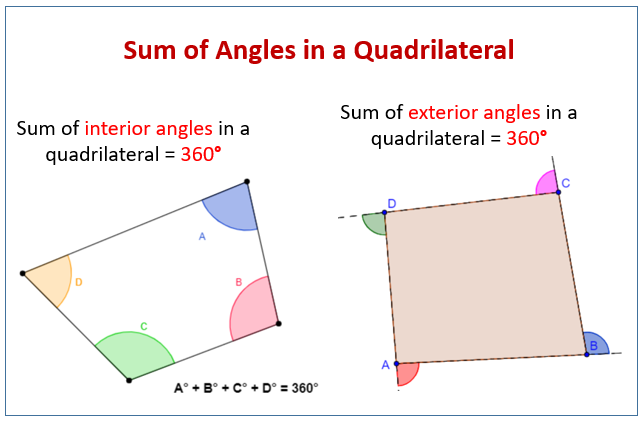
Interior And Exterior Angles Of Quadrilaterals Examples Solutions In this case, 'n' = 6. therefore, the sum of the interior angles of a hexagon = s = (n − 2) × 180° = (6 − 2) × 180° = 4 × 180° = 720°. what is the angle sum property of a quadrilateral? according to the angle sum property of a quadrilateral, the sum of all its four interior angles is 360°. this can be calculated by the formula, s. Sum of interior angles of a quadrilateral $= 360^{\circ}$ note: if 3 angles of a quadrilateral are known, then the 4th angle can be calculated using the formula: $360^{\circ} \; \;$ (sum of the other 3 interior angles). interior angle and corresponding exterior angle. the sum of an interior angle and its corresponding exterior angle is always 180. Hence, the sum of all the four angles of a quadrilateral is 360°. solved examples of angle sum property of a quadrilateral: 1. the angle of a quadrilateral are (3x 2)°, (x – 3), (2x 1)°, 2(2x 5)° respectively. find the value of x and the measure of each angle. solution:. Mistaking the sum of angles in a quadrilateral with the angles in a triangle; the angle sum is remembered incorrectly as 180° , rather than 360° . the sum of angles in a triangle is equal to 180° . join all the diagonals; when recalling the angle sum in a quadrilateral, students join all the diagonals together, creating 4 triangles.
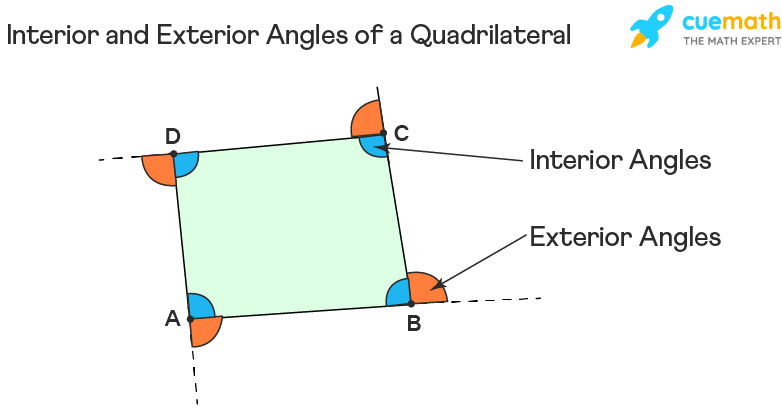
Angles Of Quadrilateral Formula Properties Examples Hence, the sum of all the four angles of a quadrilateral is 360°. solved examples of angle sum property of a quadrilateral: 1. the angle of a quadrilateral are (3x 2)°, (x – 3), (2x 1)°, 2(2x 5)° respectively. find the value of x and the measure of each angle. solution:. Mistaking the sum of angles in a quadrilateral with the angles in a triangle; the angle sum is remembered incorrectly as 180° , rather than 360° . the sum of angles in a triangle is equal to 180° . join all the diagonals; when recalling the angle sum in a quadrilateral, students join all the diagonals together, creating 4 triangles. The sum of the interior angles of a quadrilateral is always 360 360 degrees, while for other polygons, the sum is calculated using the formula (n−2)×180 (n−2) × 180 degrees, where n n is the number of sides. for example, a triangle’s angles add up to 180 180 degrees, and a pentagon’s angles add up to 540 540 degrees. A quadrilateral is a polygon with four sides, four interior angles and eight exterior angles. there are various types of quadrilaterals and all of them follow the angle sum property of quadrilaterals. the angle sum property of a quadrilateral states that the sum of all interior angles of a quadrilateral is \(360^\circ \). in this article we.

Learnhive Icse Grade 8 Mathematics Quadrilaterals Lessons The sum of the interior angles of a quadrilateral is always 360 360 degrees, while for other polygons, the sum is calculated using the formula (n−2)×180 (n−2) × 180 degrees, where n n is the number of sides. for example, a triangle’s angles add up to 180 180 degrees, and a pentagon’s angles add up to 540 540 degrees. A quadrilateral is a polygon with four sides, four interior angles and eight exterior angles. there are various types of quadrilaterals and all of them follow the angle sum property of quadrilaterals. the angle sum property of a quadrilateral states that the sum of all interior angles of a quadrilateral is \(360^\circ \). in this article we.
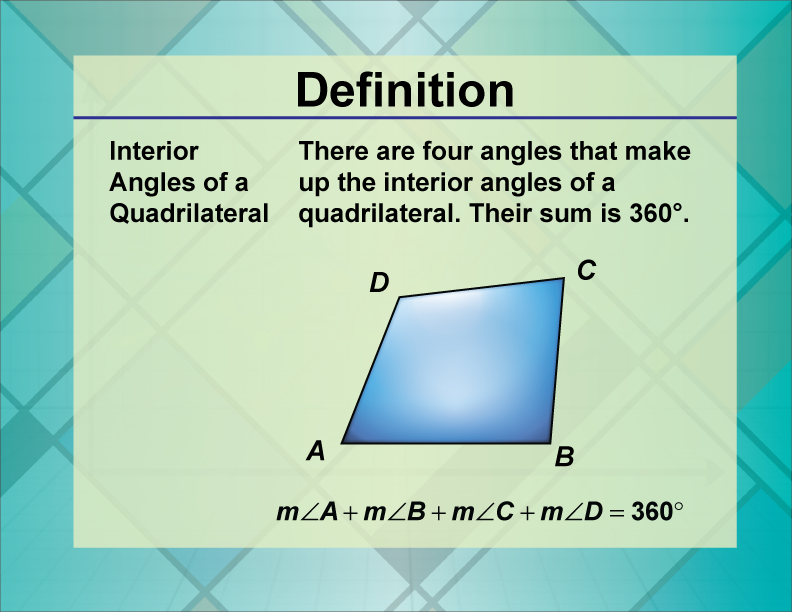
Definition Quadrilateral Concepts Interior Angles Of A Quadrilateral

Comments are closed.